
分析 由矩阵的运算性质|A|=$(\frac{1}{2})^{3}$×2×(1×5-2×3),求得|A|,再求出A的转置矩阵,由A-1=$\frac{1}{丨A丨}$×A*,求出,A-1,根据矩阵A*丨I进行初等行变换即可求得(A*)-1.
解答 解:A=$\frac{1}{2}$$(\begin{array}{l}{2}&{0}&{0}\\{0}&{1}&{3}\\{0}&{2}&{5}\end{array})$,设B=$(\begin{array}{l}{2}&{0}&{0}\\{0}&{1}&{3}\\{0}&{2}&{5}\end{array})$,
|A|=$(\frac{1}{2})^{3}$×2×(1×5-2×3)=-$\frac{1}{4}$,
A11=($\frac{1}{2}$)2$|\begin{array}{l}{1}&{3}\\{2}&{5}\end{array}|$=-$\frac{1}{4}$,A12=-($\frac{1}{2}$)2$|\begin{array}{l}{0}&{3}\\{0}&{5}\end{array}|$=0,A13=($\frac{1}{2}$)2$|\begin{array}{l}{0}&{1}\\{0}&{2}\end{array}|$=0,
A21=-($\frac{1}{2}$)2$|\begin{array}{l}{0}&{0}\\{2}&{5}\end{array}|$=0,A22=($\frac{1}{2}$)2$|\begin{array}{l}{2}&{0}\\{0}&{5}\end{array}|$=$\frac{5}{2}$,A23=-($\frac{1}{2}$)2$|\begin{array}{l}{2}&{0}\\{0}&{2}\end{array}|$=-1,
A31=($\frac{1}{2}$)2$|\begin{array}{l}{0}&{0}\\{1}&{3}\end{array}|$=0,A32=-($\frac{1}{2}$)2$|\begin{array}{l}{2}&{0}\\{0}&{3}\end{array}|$=-$\frac{3}{2}$,A33=($\frac{1}{2}$)2$|\begin{array}{l}{2}&{0}\\{0}&{1}\end{array}|$=$\frac{1}{2}$,
∴A*=$[\begin{array}{l}{-\frac{1}{4}}&{0}&{0}\\{0}&{\frac{5}{2}}&{-\frac{3}{2}}\\{0}&{-1}&{\frac{1}{2}}\end{array}]$,
∴A-1=$\frac{1}{丨A丨}$×A*=-4×$[\begin{array}{l}{-\frac{1}{4}}&{0}&{0}\\{0}&{\frac{5}{2}}&{-\frac{3}{2}}\\{0}&{-1}&{\frac{1}{2}}\end{array}]$=$[\begin{array}{l}{1}&{0}&{0}\\{0}&{-10}&{6}\\{0}&{4}&{-2}\end{array}]$,
∵(A*丨I)=$[\begin{array}{l}{\frac{1}{4}}&{0}&{0}&{1}&{0}&{0}\\{0}&{\frac{5}{2}}&{\frac{3}{2}}&{0}&{1}&{0}\\{0}&{-1}&{\frac{1}{2}}&{0}&{0}&{1}\end{array}]$→$[\begin{array}{l}{1}&{0}&{0}&{-4}&{0}&{0}\\{0}&{1}&{\frac{3}{5}}&{0}&{\frac{2}{5}}&{0}\\{0}&{0}&{\frac{1}{10}}&{0}&{\frac{2}{5}}&{1}\end{array}]$→$[\begin{array}{l}{1}&{0}&{0}&{-4}&{0}&{0}\\{0}&{1}&{0}&{0}&{-2}&{-6}\\{0}&{0}&{1}&{0}&{-4}&{-10}\end{array}]$,
∴(A*)-1=$[\begin{array}{l}{-4}&{0}&{0}\\{0}&{-2}&{-6}\\{0}&{-4}&{-10}\end{array}]$.
点评 本题考查逆变换及逆矩阵,考查求|A|,转置矩阵及逆矩阵的方法,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-2y+3=0 | B. | 2x-y+3=0 | C. | 2x-4y+5=0 | D. | 2x+y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,ABCD是直角梯形,AB∥CD,BC⊥CD,CF⊥平面ABCD,DE∥CF,AD⊥DB.
如图,ABCD是直角梯形,AB∥CD,BC⊥CD,CF⊥平面ABCD,DE∥CF,AD⊥DB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
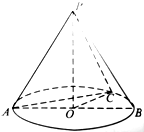 如图,在圆锥PO中,已知PO=$\sqrt{2}$,⊙O的直径AB=2,C是$\widehat{AB}$的中点,则二面角B-PA-C的余弦值为( )
如图,在圆锥PO中,已知PO=$\sqrt{2}$,⊙O的直径AB=2,C是$\widehat{AB}$的中点,则二面角B-PA-C的余弦值为( )| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{\sqrt{10}}{5}$ | C. | $\frac{\sqrt{15}}{5}$ | D. | $\sqrt{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com