

分析 如图所示,设正方体的棱长为a.由于${V}_{P-AB{A}^{′}}$=$\frac{1}{6}{a}^{3}$是一个定值,设点B到平面PAA′距离为h,则$\frac{1}{6}{a}^{3}$=$\frac{1}{3}h•{S}_{△A{A}^{′}P}$,可得h=$\frac{{a}^{2}}{{A}^{′}P}$,因此A′P取得最大值时,h取得最小值.
解答 解:如图所示,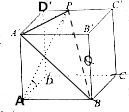 设正方体的棱长为a.
设正方体的棱长为a.
由于${V}_{P-AB{A}^{′}}$=$\frac{1}{3}×\frac{1}{2}{a}^{2}×a$=$\frac{1}{6}{a}^{3}$是一个定值,
设点B到平面PAA′距离为h,
则$\frac{1}{6}{a}^{3}$=$\frac{1}{3}h•{S}_{△A{A}^{′}P}$,${S}_{△A{A}^{′}P}$=$\frac{1}{2}a•{A}^{′}P$,
∴h=$\frac{{a}^{2}}{{A}^{′}P}$,
因此当A′P取得最大值A′C′=$\sqrt{2}a$时,h取得最小值$\frac{\sqrt{2}}{2}$a.
∴tan∠PAD=$\frac{AD}{{C}^{′}D}$=$\frac{a}{\sqrt{2}a}$=$\frac{\sqrt{2}}{2}$,
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题考查了线面面面垂直的判定与性质定理、正方体的性质、三棱锥的体积计算公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
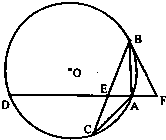 如图,△ABC内接于圆O,AB=AC,AD⊥AB,AD交BC于点E,点F在DA的延长线上,AF=AE.求证:
如图,△ABC内接于圆O,AB=AC,AD⊥AB,AD交BC于点E,点F在DA的延长线上,AF=AE.求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在直三棱柱ABA1中,D1C=$\sqrt{2}$a,DD1=DA=DC=a,点E、F分别是BC、DC的中点.
如图,在直三棱柱ABA1中,D1C=$\sqrt{2}$a,DD1=DA=DC=a,点E、F分别是BC、DC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 一年级 | 二年级 | 三年级 | |
| 女生 | 373 | x | y |
| 男生 | 377 | 370 | z |
| 优秀 | 不优秀 | |
| 甲班 | 10 | 30 |
| 乙班 | 12 | 28 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2,072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com