
分析 (1)根据圆的面积最大时半径最大,写出圆C1半径r的解析式,求出半径最大值以及对应的圆C1的方程,再化为标准方程;
(2)求出圆C1的圆心坐标关于直线l的对称点,即可写出对称圆圆C2的方程.
解答 解:(1)圆C1的面积最大,即圆的半径最大,
则圆C1的半径为$r=\frac{1}{2}\sqrt{{D^2}+{E^2}-4F}=\frac{1}{2}\sqrt{-4{m^2}+8m+12}=\sqrt{-{m^2}+2m+3}$,
即$r=\sqrt{-{{(m-1)}^2}+4}$,
因此当m=1时圆C1的半径最大,最大值为2,…(3分)
此时圆C1的方程为x2+y2-4x+2y+1=0,
化为标准方程是(x-2)2+(y+1)2=4;…(6分)
(2)由(1)知圆C1的圆心坐标是(2,-1),半径为2,设圆C2的圆心为(a,b),
则C1C2的中点坐标为$(\frac{a+2}{2},\frac{b-1}{2})$,直线C1C2的斜率为${k_{{c_1}{c_2}}}=\frac{b+1}{a-2}$,…..(9分)
由题意,直线l垂直平分线段C1C2,
∴$\left\{{\begin{array}{l}{\frac{a+2}{2}-\frac{b-1}{2}+1=0}\\{\frac{b+1}{a-2}=-1}\end{array}}\right.$,
解得$\left\{{\begin{array}{l}{a=-2}\\{b=3}\end{array}}\right.$;…(12分)
所以,所求圆C2的方程为(x+2)2+(y-3)2=4.…(13分)
点评 本题考查了直线与圆的方程的应用问题,也考查了求点关于直线对称点的应用问题,是综合性题目.


科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{4}$,$\frac{1}{2}}$) | B. | ($\frac{1}{4}$,$\frac{1}{2}$) | C. | [$\frac{1}{2}$,1) | D. | ($\frac{1}{2}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 当a≥$\frac{1}{2}$时,函数y=f(x)有零点 | B. | 若函数y=f(x)有零点,则a≥$\frac{1}{2}$ | ||
| C. | 存在a<0,使函数y=f(x)有唯一零点 | D. | 若函数y=f(x)有唯一零点,则a≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2或-$\frac{1}{2}$ | B. | -2或-$\frac{1}{2}$ | C. | -2或$\frac{1}{2}$ | D. | 2或$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
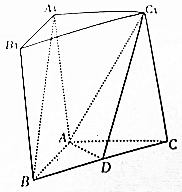 如图,在直三棱柱A1B1C1-ABC中,AB⊥AC,AA1=2AB=2AC,点D是BC的中点.
如图,在直三棱柱A1B1C1-ABC中,AB⊥AC,AA1=2AB=2AC,点D是BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com