
分析 (1)由直线与圆相切,得圆心到直线的距离d=r,列出方程求出a的值,从而求出直线l的方程;
(2)利用AB的中点M,结合OB=2OA,设出所求直线的方程,利用圆心到直线l的距离d和勾股定理,可以求出l的方程;
(3)设A,B两点的纵坐标分别为y1,y2,求出点D的坐标,写出△ABD的面积f(t),利用直线AB的方程与圆的方程联立,结合根与系数的关系,即可求出f(t)的解析式.
解答 解:(1)由直线m:ax-2y+a+2=0(a>0)与圆C:x2+y2-4x-1=0相切,
得圆心C(2,0)到直线的距离d=r=$\sqrt{5}$,
即$\frac{{|{3a+2}|}}{{\sqrt{{a^2}+4}}}=\sqrt{5}$,
化简得:a2+3a-4=0,
解得a=1或a=-4,
由于a>0,故a=1;
由直线m与圆解得切点B(1,2),得l:y=2x;(3分)
(2)取AB的中点M,则AM=$\frac{1}{2}$AB,
又$OA=\frac{1}{3}AB$,所以$OM=\frac{1}{3}AM$,
设:OM=x,圆心到直线l的距离为d,
由勾股定理得:x2+d2=4,9x2+d2=5,解得${d^2}=\frac{31}{8}$,
设所求直线的方程为y=kx,$d=\frac{{|{2k}|}}{{\sqrt{1+{k^2}}}}$,
解得$k=±\sqrt{31}$,直线$l:y=±\sqrt{31}x$;(8分)
(3)如图:设A,B两点的纵坐标分别为y1,y2,
易知$D(2+\sqrt{5},0)$,${S_{△ABD}}=\frac{1}{2}(2+\sqrt{5})(|{y_1}|+|{y_2}|)$,
易知|y1|+|y2|=|y1-y2|,
设AB的方程为x=ty,
由$\left\{\begin{array}{l}x=ty\\{x^2}+{y^2}-4x-1=0\end{array}\right.$,消元得(t2+1)y2-4ty-1=0,
$|{{y_1}-{y_2}}|=\frac{{\sqrt{△}}}{{1+{t^2}}}=\frac{{\sqrt{20{t^2}+4}}}{{1+{t^2}}}$=$2\sqrt{\frac{{5{t^2}+1}}{{{{({t^2}+1)}^2}}}}$,
则 $f(t)=2\sqrt{\frac{{5{t^2}+1}}{{{{({t^2}+1)}^2}}}}(t∈R)$.(12分)
点评 本题考查了直线与圆的方程的应用问题,也考查了函数与方程思想的综合应用问题,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{37}$-1 | B. | $\frac{8\sqrt{5}}{5}$ | C. | $\frac{8\sqrt{5}-5}{5}$ | D. | $\sqrt{37}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 男生 | 女生 | 合计 | |
| 偏理科 | 28 | 16 | 44 |
| 偏文科 | 4 | 8 | 12 |
| 合计 | 32 | 24 | 56 |
| P(K2>k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
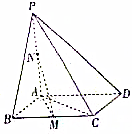 如图.在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥平面ABCD,点M,N分别为BC,PA的中点,且AB=AC=1.
如图.在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥平面ABCD,点M,N分别为BC,PA的中点,且AB=AC=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在直三棱柱ABA1中,D1C=$\sqrt{2}$a,DD1=DA=DC=a,点E、F分别是BC、DC的中点.
如图,在直三棱柱ABA1中,D1C=$\sqrt{2}$a,DD1=DA=DC=a,点E、F分别是BC、DC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com