
| 男生 | 女生 | 合计 | |
| 偏理科 | 28 | 16 | 44 |
| 偏文科 | 4 | 8 | 12 |
| 合计 | 32 | 24 | 56 |
| P(K2>k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)求出K2=3.535>2.706,从而有90%的把握认为科目偏向与性别有关.
(2)按分层抽样的方法选出14人,偏理科的人数为$\frac{14}{56}×44=11$,偏文科的人数为$\frac{14}{56}×12=3$.由此利用组合知识可以求出概率.
(3)按分层抽样的方法选出14人,男生人数为$\frac{14}{56}×32=8$,女生人数为$\frac{14}{56}×24=6$.设一次选出2人中选到男生人数为X,则X所有可能的取值为0,1,2.求出相应的概率,即可求一次选出的2人中男生人数X的分布列及期望.
解答 解:(1)${k^2}=\frac{{56{{({28×8-16×4})}^2}}}{44×12×32×24}=3,535>2.706$.所以有90%的把握认为科目偏向与性别有关.
(2)按分层抽样的方法选出14人,偏理科的人数为$\frac{14}{56}×44=11$,偏文科的人数为$\frac{14}{56}×12=3$.
记“在这14人中选2人偏文科”为事件A.则$P(A)=\frac{C_3^2}{{C_{14}^2}}=\frac{3}{91}$.
(3)按分层抽样的方法选出14人,男生人数为$\frac{14}{56}×32=8$,女生人数为$\frac{14}{56}×24=6$.
设一次选出2人中选到男生人数为X,则X所有可能的取值为0,1,2.$P({X=0})=\frac{C_8^0C_6^2}{{C_{14}^2}}=\frac{15}{91},P({X=1})=\frac{C_8^1C_6^1}{{C_{14}^2}}=\frac{48}{91},P({X=2})=\frac{C_8^2C_6^0}{{C_{14}^2}}=\frac{28}{91}$,
X的分布列为
| X | 0 | 1 | 2 |
| P | $\frac{15}{91}$ | $\frac{48}{91}$ | $\frac{28}{91}$ |
点评 本题考查独立检验的应用,考查概率的求法,考查分布列及期望,正确求出概率是关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 当a≥$\frac{1}{2}$时,函数y=f(x)有零点 | B. | 若函数y=f(x)有零点,则a≥$\frac{1}{2}$ | ||
| C. | 存在a<0,使函数y=f(x)有唯一零点 | D. | 若函数y=f(x)有唯一零点,则a≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2或-$\frac{1}{2}$ | B. | -2或-$\frac{1}{2}$ | C. | -2或$\frac{1}{2}$ | D. | 2或$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
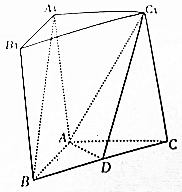 如图,在直三棱柱A1B1C1-ABC中,AB⊥AC,AA1=2AB=2AC,点D是BC的中点.
如图,在直三棱柱A1B1C1-ABC中,AB⊥AC,AA1=2AB=2AC,点D是BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
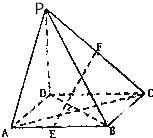 如图,在四棱锥P-ABCD中,PD⊥ABCD,底面是菱形,设DA=DP=4,E,F分别为AB,PC的中点.
如图,在四棱锥P-ABCD中,PD⊥ABCD,底面是菱形,设DA=DP=4,E,F分别为AB,PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3+$\sqrt{2}$ | B. | 2+$\sqrt{3}$ | C. | 2+$\sqrt{2}$ | D. | 3+$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com