
分析 (1)由x2-2x+a>0恒成立,可得△<0,由此求解a的取值范围;
(2)由函数y=log${\;}_{\frac{1}{2}}$(x2-2x+a)的值域为R,得二次三项式x2-2x+a能够取到大于0的所有实数,可得△≥0,进一步求解不等式得a的取值范围.
解答 解:(1)∵函数log${\;}_{\frac{1}{2}}$(x2-2x+a)的定义域为R,
∴对任意实数x,x2-2x+a>0恒成立,则△=(-2)2-4a<0,解得a>1;
(2)∵函数y=log${\;}_{\frac{1}{2}}$(x2-2x+a)的值域为R,
∴二次三项式x2-2x+a能够取到大于0的所有实数,
则△=(-2)2-4a≥0,解得a≤1.
点评 本题考查函数的定义域与值域的求法,考查数学转化思想方法,关键是对题意的理解,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{37}$-1 | B. | $\frac{8\sqrt{5}}{5}$ | C. | $\frac{8\sqrt{5}-5}{5}$ | D. | $\sqrt{37}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 男生 | 女生 | 合计 | |
| 偏理科 | 28 | 16 | 44 |
| 偏文科 | 4 | 8 | 12 |
| 合计 | 32 | 24 | 56 |
| P(K2>k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
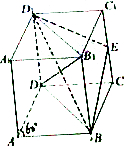 如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,∠BAD=60°,四边形BDD1B1是正方形.E是棱CC1的中点.
如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,∠BAD=60°,四边形BDD1B1是正方形.E是棱CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
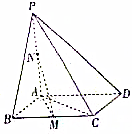 如图.在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥平面ABCD,点M,N分别为BC,PA的中点,且AB=AC=1.
如图.在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥平面ABCD,点M,N分别为BC,PA的中点,且AB=AC=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [15,+∞) | B. | [6,+∞) | C. | (-∞,15] | D. | (-∞,6] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
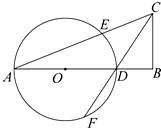 如图,已知△ABC中,B=90°,∠C的平分线交AB于D,以AD为直径的圆O交AC于点E、交CD于点F.
如图,已知△ABC中,B=90°,∠C的平分线交AB于D,以AD为直径的圆O交AC于点E、交CD于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com