
| A. | [15,+∞) | B. | [6,+∞) | C. | (-∞,15] | D. | (-∞,6] |
分析 由不等式进行转化判断函数的单调性,求函数的导数,利用参数分离法 进行求解即可.
解答 解:因为p≠q,不妨设p>q,由于$\frac{{f({p+1})-f({q+1})}}{p-q}>1$,
所以f(p+1)-f(q+1)>p-q,得[f(p+1)-(p+1)]-[f(q+1)-(q+1)]>0,
因为p>q,所以p+1>q+1,所以g(x)=f(x+1)-(x+1)在(0,1)内是增函数,
所以g'(x)>0在(0,1)内恒成立,即$\frac{a}{x+2}-(2x+3)>0$恒成立,
所以a>(2x+3)(x+2)的最大值,
因为x∈(0,1)时(2x+3)(x+2)<15,
所以实数a的取值范围为[15,+∞).
故选:A.
点评 本题主要考查不等式恒成立问题,根据不等式进行转化判断函数的单调性,结合参数分离法进行转化是解决本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
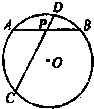
| A. | 5 | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
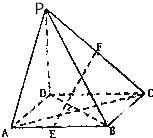 如图,在四棱锥P-ABCD中,PD⊥ABCD,底面是菱形,设DA=DP=4,E,F分别为AB,PC的中点.
如图,在四棱锥P-ABCD中,PD⊥ABCD,底面是菱形,设DA=DP=4,E,F分别为AB,PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
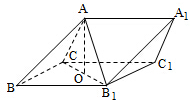 如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C.
如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
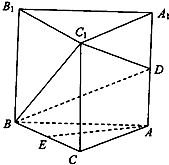 如图,三棱柱ABC-A1B1C1中,D为AA1的中点,E为BC的中点,
如图,三棱柱ABC-A1B1C1中,D为AA1的中点,E为BC的中点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
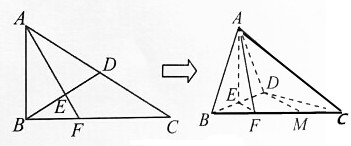 如图,△ABC中,∠ABC=90°,∠C=30°,AB=1,D为AC中点,AE⊥BD于点E,延长AE交BC于点F,沿BD将△ABC折成四面体A-BCD.
如图,△ABC中,∠ABC=90°,∠C=30°,AB=1,D为AC中点,AE⊥BD于点E,延长AE交BC于点F,沿BD将△ABC折成四面体A-BCD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com