
分析 由题意可设A(1,0),B(0,1),对于①,可得P的坐标和直线l的方程,由中点坐标公式即可判断;
对于②,当k<-1时,求得直线l的斜率范围,可得直线l与BA的延长线有交点,即可判断;
对于③,当k=-1时,求得直线AB的斜率和直线l的斜率,由两直线平行的条件,即可判断;
对于④,运用两直线垂直的条件:斜率之积为-1,结合新定义即可判断;
对于⑤,运用两直线的夹角公式,结合新定义即可判断.
解答 解:平面内$\overrightarrow{OA}$与$\overrightarrow{OB}$是一组不平行向量,且|$\overrightarrow{OA}}$|=|${\overrightarrow{OB}}$|=1,$\overrightarrow{OA}⊥\overrightarrow{OB}$,
可设A(1,0),B(0,1),
①当k=1时,有λ1=λ2,$\overrightarrow{OP}$=λ1$\overrightarrow{OA}$+λ2$\overrightarrow{OB}$=(λ1,λ2),
即有P在直线y=x上,直线l经过线段AB中点($\frac{1}{2}$,$\frac{1}{2}$),故①正确;
②当k<-1时,直线l的方程为y=$\frac{{λ}_{2}}{{λ}_{1}}$x,可得直线l的斜率为(-1,0),
即有直线l与BA的延长线有交点,故②不正确;
③当k=-1时,直线l为y=-x,kAB=$\frac{1-0}{0-1}$=-1,直线l与AB平行,故③正确;
④l1⊥l2时,可得直线l1,l2的斜率之积为-1,由新定义可得对应的等商比满足k1•k2=-1,故④正确;
⑤直线l1与l2的夹角记为θ(θ≠$\frac{π}{2}}$)对应的等商比为k1、k2,
由两直线的夹角公式可得tanθ=|$\frac{\frac{1}{{k}_{1}}-\frac{1}{{k}_{2}}}{1+\frac{1}{{k}_{1}{k}_{2}}}$|,化简可得tanθ=$\frac{{|{{k_1}-{k_2}}|}}{{|{1+{k_1}{k_2}}|}}$.故⑤正确.
故答案为:①③④⑤.
点评 本题考查新定义的理解和运用,注意运用转化思想和坐标法,两直线平行、垂直的条件,以及夹角公式,考查化简整理的运算能力,属于中档题.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:选择题
| A. | [15,+∞) | B. | [6,+∞) | C. | (-∞,15] | D. | (-∞,6] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
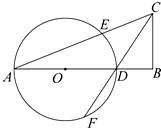 如图,已知△ABC中,B=90°,∠C的平分线交AB于D,以AD为直径的圆O交AC于点E、交CD于点F.
如图,已知△ABC中,B=90°,∠C的平分线交AB于D,以AD为直径的圆O交AC于点E、交CD于点F.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | -2$\sqrt{3}$ | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
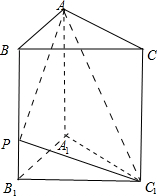 已知直三棱柱ABC-A1B1C1中,AB⊥AC,AB=3,AC=4,B1C⊥AC1.
已知直三棱柱ABC-A1B1C1中,AB⊥AC,AB=3,AC=4,B1C⊥AC1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com