
分析 (I)曲线C1的参数方程为$\left\{\begin{array}{l}{x=2cosθ}\\{y=\sqrt{3}sinθ}\end{array}\right.$(θ为参数),利用cos2θ+sin2θ=1即可得出普通方程.曲线C2的极坐标方程是$\sqrt{2}$ρsin(θ-$\frac{π}{4}$)=1,利用和差公式展开可得:$\sqrt{2}×\frac{\sqrt{2}}{2}$ρ(sinθ-cosθ)=1,即可得出直角坐标方程.
(2)通过M,N两点的圆中面积最小的圆是以|MN|为直径的圆的方程.设M(x1,y1),N(x2,y2),直线方程与圆的方程联立可得:7x2+8x-8=0,利用根与系数的关系、弦长公式即可得出.
解答 解:(I)曲线C1的参数方程为$\left\{\begin{array}{l}{x=2cosθ}\\{y=\sqrt{3}sinθ}\end{array}\right.$(θ为参数),可得$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,
曲线C2的极坐标方程是$\sqrt{2}$ρsin(θ-$\frac{π}{4}$)=1,展开可得:$\sqrt{2}×\frac{\sqrt{2}}{2}$ρ(sinθ-cosθ)=1,可得直角坐标方程:y-x=1.
(2)通过M,N两点的圆中面积最小的圆是以|MN|为直径的圆的方程.
设M(x1,y1),N(x2,y2),
联立$\left\{\begin{array}{l}{y-x=1}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,化为:7x2+8x-8=0,
∴x1+x2=-$\frac{8}{7}$,x1x2=-$\frac{8}{7}$.
∴|MN|=$\sqrt{2[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$=$\sqrt{2[(-\frac{8}{7})^{2}-4×(-\frac{8}{7})]}$=$\frac{8\sqrt{3}}{7}$.
$\frac{{x}_{1}+{x}_{2}}{2}$=$-\frac{4}{7}$,$\frac{{y}_{1}+{y}_{2}}{2}$=$\frac{{x}_{1}+{x}_{2}+2}{2}$=$\frac{3}{7}$,
∴圆心$(-\frac{4}{7},\frac{3}{7})$,
∴通过M,N两点的圆中面积最小的圆的标准方程为:$(x+\frac{4}{7})^{2}$+$(y-\frac{3}{7})^{2}$=$\frac{192}{49}$.
点评 本题考查了极坐标与直角坐标的互化、参数方程化为普通方程、直线与椭圆相交弦长问题、中点坐标公式、圆的标准方程,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
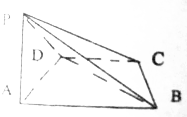 如图,在四棱锥P-ACD中,底面ABCD为等腰梯形,且满足AB∥CD,AD=DC=$\frac{1}{2}$AB=1,PA=$\sqrt{2}$,PA⊥平面ABCD.
如图,在四棱锥P-ACD中,底面ABCD为等腰梯形,且满足AB∥CD,AD=DC=$\frac{1}{2}$AB=1,PA=$\sqrt{2}$,PA⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com