
分析 (1)求出OC的长度,得到d的范围,再由垂径定理把弦长用d表示,可得△OPQ的面积S的表达式;
(2)利用基本不等式求得S的最大值,得到相应的d值,再由点到直线距离公式求得直线的斜率得答案.
解答 解:(1)如图,
∵圆内一点C(2,1),∴|OC|=$\sqrt{5}$,
则圆心O到直线l的距离为d∈(0,$\sqrt{5}$].
∵圆O的半径为3,∴|PQ|=2$\sqrt{9-{d}^{2}}$,
则S(d)=$\frac{1}{2}|PQ|•d=\frac{1}{2}×2\sqrt{9-{d}^{2}}•d$=$\sqrt{(9-{d}^{2})•{d}^{2}}$.
函数定义域为(0,$\sqrt{5}$];
(2)由S(d)=$\sqrt{(9-{d}^{2})•{d}^{2}}$$≤\sqrt{(\frac{9-{d}^{2}+{d}^{2}}{2})^{2}}$=$\frac{9}{2}$.
得S的最大值为$\frac{9}{2}$,当且仅当9-d2=d2,即${d}^{2}=\frac{9}{2}$,d=$\frac{3\sqrt{2}}{2}$∈(0,$\sqrt{5}$].
此时直线l的斜率存在,设为k,则直线方程为y-1=k(x-2),即kx-y-2k+1=0.
由d=$\frac{|-2k+1|}{\sqrt{{k}^{2}+1}}=\frac{3\sqrt{2}}{2}$,解得k=-1或k=-7.
∴直线l的方程为:x+y-3=0或7x+y-15=0.
点评 本题考查直线与圆位置关系的应用,考查点到直线距离公式的应用,训练了利用基本不等式求最值,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
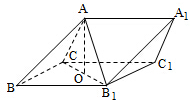 如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C.
如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 精确值 | B. | 不足近似值 | C. | 过剩近似值 | D. | 以上都有可能 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
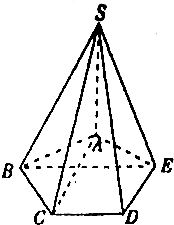 如图,在五棱锥S-ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,BC=DE=$\sqrt{3}$,∠BAE=∠BCD=∠CDE=120°
如图,在五棱锥S-ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,BC=DE=$\sqrt{3}$,∠BAE=∠BCD=∠CDE=120°查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com