
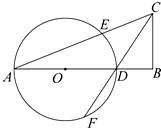
 如图,已知△ABC中,B=90°,∠C的平分线交AB于D,以AD为直径的圆O交AC于点E、交CD于点F.
如图,已知△ABC中,B=90°,∠C的平分线交AB于D,以AD为直径的圆O交AC于点E、交CD于点F.分析 (1)连接DE,则∠DEC=90°,证明C,E,D,B四点共圆,利用切割线定理证明AE•AC=AD•AB;
(2)若BD=1,BC=$\sqrt{3}$,求出CF,即可求点F到线段AC的距离.
解答 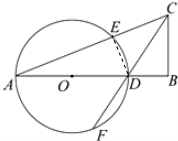 证明:(1)连接DE,则∠DEC=90°,
证明:(1)连接DE,则∠DEC=90°,
∵∠B=90°,
∴C,E,D,B四点共圆,
∴AE•AC=AD•AB;
解:(2)若BD=1,BC=$\sqrt{3}$,
则∠DCB=30°,∠ACB=60°,
∴AC=2$\sqrt{3}$,CE=$\sqrt{3}$,CD=2,
∵CE•CA=CD•CF,
∴CF=3,
∴点F到线段AC的距离为$\frac{3}{2}$.
点评 本题主要考查与圆有关的比例线段和切割线定理,证明乘积式的问题,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
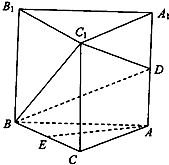 如图,三棱柱ABC-A1B1C1中,D为AA1的中点,E为BC的中点,
如图,三棱柱ABC-A1B1C1中,D为AA1的中点,E为BC的中点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
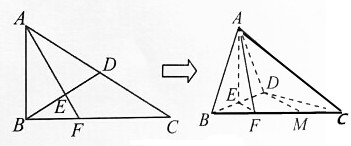 如图,△ABC中,∠ABC=90°,∠C=30°,AB=1,D为AC中点,AE⊥BD于点E,延长AE交BC于点F,沿BD将△ABC折成四面体A-BCD.
如图,△ABC中,∠ABC=90°,∠C=30°,AB=1,D为AC中点,AE⊥BD于点E,延长AE交BC于点F,沿BD将△ABC折成四面体A-BCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3+$\sqrt{2}$ | B. | 2+$\sqrt{3}$ | C. | 2+$\sqrt{2}$ | D. | 3+$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-∞,}\right.-\sqrt{2})∪(\sqrt{2},+∞)$ | B. | (-3$\sqrt{2}$,-$\sqrt{2}$)∪($\sqrt{2}$,3$\sqrt{2}$) | C. | $(-3\sqrt{2},3\sqrt{2})$ | D. | $(-\sqrt{2},\sqrt{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com