
分析 由x的范围求出|f(x)-g(x)|的范围,由其最大值小于等于1求得a的范围,可得当1<a<6时,f(x)与g(x)在给区间[0,1]上是“非接近”的;当a≥6时,f(x)与g(x)在给区间[0,1]上是“接近”的.
解答 解:|f(x)-g(x)|=|loga(x+2)-loga$\frac{1}{x+1}$|=|loga(x+1)(x+2)|.
令t=(x+1)(x+2).
当x∈[0,1]时,t∈[2,6].
∵a>1,∴|loga(x+1)(x+2)|=|logat|=logat∈[loga2,loga6].
由loga6≤1,得a≥6.
∴当1<a<6时,f(x)与g(x)在给区间[0,1]上是“非接近”的;
当a≥6时,f(x)与g(x)在给区间[0,1]上是“接近”的.
点评 本题考查对数函数的性质和应用,对题意的理解是解答该题的关键,属中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
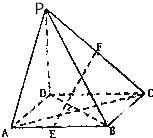 如图,在四棱锥P-ABCD中,PD⊥ABCD,底面是菱形,设DA=DP=4,E,F分别为AB,PC的中点.
如图,在四棱锥P-ABCD中,PD⊥ABCD,底面是菱形,设DA=DP=4,E,F分别为AB,PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3+$\sqrt{2}$ | B. | 2+$\sqrt{3}$ | C. | 2+$\sqrt{2}$ | D. | 3+$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-∞,}\right.-\sqrt{2})∪(\sqrt{2},+∞)$ | B. | (-3$\sqrt{2}$,-$\sqrt{2}$)∪($\sqrt{2}$,3$\sqrt{2}$) | C. | $(-3\sqrt{2},3\sqrt{2})$ | D. | $(-\sqrt{2},\sqrt{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-2y+3=0 | B. | 2x-y+3=0 | C. | 2x-4y+5=0 | D. | 2x+y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,ABCD是直角梯形,AB∥CD,BC⊥CD,CF⊥平面ABCD,DE∥CF,AD⊥DB.
如图,ABCD是直角梯形,AB∥CD,BC⊥CD,CF⊥平面ABCD,DE∥CF,AD⊥DB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com