
分析 把m=(ab+cd)2-$\frac{1}{4}$(a2+b2-c2-d2)2进行因式分解,再由因式分解的结果及合数的定义进行解答.
解答 证明:要证明|m|是合数,只要能证出|m|=p•q,p•q均为大于1的正整数即可.
m=(ab+cd)2-$\frac{1}{4}$(a2+b2-c2-d2)2,
=[ab+cd+$\frac{1}{2}$(a2+b2-c2-d2)]•[ab+cd-$\frac{1}{2}$(a2+b2-c2-d2)],
=$\frac{1}{4}$(2ab+2cd+a2+b2-c2-d2)•(2ab+2cd-a2-b2+c2+d2),
=$\frac{1}{4}$[(a+b)2-(c-d)2]•[(c+d)2-(a-b)2],
=$\frac{1}{4}$(a+b+c-d)(a+b-c+d)(c+d+a-b)(c+d-a+b)
因为m是非零整数,则 $\frac{1}{4}$(a+b+c-d)(a+b-c+d)(c+d+a-b)(c+d-a+b)是非零整数.
由于四个数a+b+c-d,a+b-c+d,a-b+c+d,-a+b+c+d的奇偶性相同,乘积应被4整除,
所以四个数均为偶数.
所以可设a+b+c-d=2m1,a+b-c+d=2m2,a-b+c+d=2m3,-a+b+c+d=2m4,其中m1,m2,m3,m4均为非零整数.
所以m=(2m1)(2m2)(2m3)(2m4)=4m1m2m3m4,
所以|m|=4|m1m2m3m4|≠0,
所以|m|是一个合数.
点评 本题考查的是质数与合数的定义、因式分解、奇数与偶数的定义、绝对值的性质,涉及面较广,难度较大


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 当a≥$\frac{1}{2}$时,函数y=f(x)有零点 | B. | 若函数y=f(x)有零点,则a≥$\frac{1}{2}$ | ||
| C. | 存在a<0,使函数y=f(x)有唯一零点 | D. | 若函数y=f(x)有唯一零点,则a≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
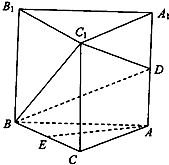 如图,三棱柱ABC-A1B1C1中,D为AA1的中点,E为BC的中点,
如图,三棱柱ABC-A1B1C1中,D为AA1的中点,E为BC的中点,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com