
| A. | 当a≥$\frac{1}{2}$时,函数y=f(x)有零点 | B. | 若函数y=f(x)有零点,则a≥$\frac{1}{2}$ | ||
| C. | 存在a<0,使函数y=f(x)有唯一零点 | D. | 若函数y=f(x)有唯一零点,则a≤1 |
分析 先将方程f(x)=0进行参变量分离,得到2a=$\frac{{x}^{2}}{x+lnx}$,令g(x)=$\frac{{x}^{2}}{x+lnx}$,转化成y=2a与y=g(x)的图象的交点个数,利用导数得到函数的单调性,结合函数的图象可得A,C,D都正确,B错误.
解答 解:令f(x)=x2-2ax-2alnx=0,则2a(x+lnx)=x2,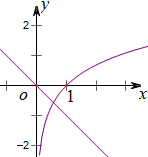
∴2a=$\frac{{x}^{2}}{x+lnx}$,令g(x)=$\frac{{x}^{2}}{x+lnx}$,
则g′(x)=$\frac{x(x-1+2lnx)}{(x+lnx)^{2}}$
令h(x)=x+lnx,通过作出两个函数y=lnx及y=-x的图象(如右图)
发现h(x)有唯一零点在(0,1)上,
设这个零点为x0,当x∈(0,x0)时,g′(x)<0,g(x)在(0,x0)上单调递减,x=x0是渐近线,
当x∈(x0,1)时,g′(x)<0,则g(x)在(x0,1)上单调递减,
当x∈(1,+∞)时g′(x)>0,g(x)在(1,+∞)单调递增,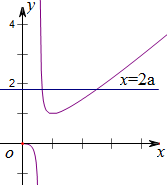
∴g(1)=1,可以作出g(x)=$\frac{{x}^{2}}{x+lnx}$的大致图象,
结合图象可知,当a<0时,y=2a与y=g(x)的图象只有一个交点,则函数y=f(x)只有一个零点,故选项A正确;
若函数y=f(x)有零点,则a<0或a≥$\frac{1}{2}$,故选项A正确,B不正确,选项C正确;
若函数y=f(x)有唯一零点,则a≤1,故选项D正确.
故选:B.
点评 本题考查了函数的零点与方程根的关系.函数的零点等价于对应方程的根,等价于函数的图象与x轴交点的横坐标,解题时要注意根据题意合理的选择转化.常运用数形结合的数学思想方法.属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 男生 | 女生 | 合计 | |
| 偏理科 | 28 | 16 | 44 |
| 偏文科 | 4 | 8 | 12 |
| 合计 | 32 | 24 | 56 |
| P(K2>k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com