
分析 (Ⅰ)求函数的导数,利用函数零点的判定定理进行判断即可.
(Ⅱ)利用不等式恒成立,转化为求函数的最值,求函数的导数,判断函数的单调性求函数的最值进行求解.
解答 (Ⅰ)证明:∵g(x)=f′(x)=ex+2ax,g′(x)=ex+2a,------------------------(1分)
当a>0时,g′(x)>0,∴函数g(x)在(-∞,+∞)上的单调递增,------------------------(2分)
又g(-$\frac{1}{2a}$)=${e}^{-\frac{1}{2a}}$-1<0,g(0)=1>0,-----------------------------------------------(3分)
∴存在唯一的x0∈(-$\frac{1}{2a}$,0),使得g(x0)=0;-----------------------------------------------(4分)
(Ⅱ)解:(1)当a<0时,则当x<0时,g(x)>0,
即函数f(x)在(-∞,0)上单调递增,且当x→-∞时,f(x)→-∞,这与f(x)≥b矛盾;---------------------------(5分)
(2)当a=0,由ex≥b,得b≤0,∴a-b≥0;------------------------------------------(6分)
(3)当a>0,由(Ⅰ)知当x∈(-∞,x0)时,g(x)<0;当x∈(x0,+∞)时,g(x)>0;
即f(x)在(-∞,x0)上单调递减,在(x0,+∞)上单调递增,----------------------------------(7分)
∴f(x)的最小值为f(x0),-----------------------------------------------------------------------------------(8分)
其中x0满足${e}^{{x}_{0}}$+2ax0=0,故a=-$\frac{{e}^{{x}_{0}}}{2{x}_{0}}$且x0<0,
∵f(x)≥b恒成立,∴b≤f(x0),
即-b≥-${e}^{{x}_{0}}$-ax02,于是a-b≥-${e}^{{x}_{0}}$-ax02=-${e}^{{x}_{0}}$(1+$\frac{1}{2{x}_{0}}$-$\frac{{x}_{0}}{2}$),------------------(9分)
记h(x)=-ex(1+$\frac{1}{2x}$-$\frac{x}{2}$),x<0,
则h′(x)=$\frac{1}{2{x}^{2}}$ex(x-1)2(x+1),-----------------(10分)
由h′(x)<0得x<-1,即函数h(x)在(-∞,-1)上单调时递减,
由h′(x)>0得-1<x<0,即函数h(x)在(-1,0)上单调递增,
∴h(x)min=h(-1)=-$\frac{1}{e}$,
综上得a-b的最小值为-$\frac{1}{e}$,此时x0=-1.--------------------------------------------------(14分)
点评 本题主要考查函数单调性和最值的应用,结合函数零点的判定定理进行转化,求函数的导数是解决本题的关键.考查学生的运算和转化能力.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:解答题
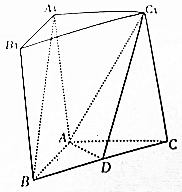 如图,在直三棱柱A1B1C1-ABC中,AB⊥AC,AA1=2AB=2AC,点D是BC的中点.
如图,在直三棱柱A1B1C1-ABC中,AB⊥AC,AA1=2AB=2AC,点D是BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3+$\sqrt{2}$ | B. | 2+$\sqrt{3}$ | C. | 2+$\sqrt{2}$ | D. | 3+$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-∞,}\right.-\sqrt{2})∪(\sqrt{2},+∞)$ | B. | (-3$\sqrt{2}$,-$\sqrt{2}$)∪($\sqrt{2}$,3$\sqrt{2}$) | C. | $(-3\sqrt{2},3\sqrt{2})$ | D. | $(-\sqrt{2},\sqrt{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-2y+3=0 | B. | 2x-y+3=0 | C. | 2x-4y+5=0 | D. | 2x+y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com