
分析 (1)求得导数,求得切线的斜率,由两直线垂直的条件:斜率之积为-1,可得a=e,进而求得f(x)的单调区间,可得极值;
(2)ax=x2(a>1)仅有1解.当x<0时,函数y=ax与函数y=x2图象恒有一个交点;由题意x>0没有交点,即ax>x2(a>1)在x>0恒成立,运用导数求得相切的情况,结合图象即可得到a的范围.
解答 解:(1)函数f(x)=ax-2x的导数为f′(x)=axlna-2,
函数f(x)在(1,f(1))处的切线斜率为alna-2,
由切线与直线x-(2-e)y+8=0垂直,可得alna-2=e-2,
解得a=e,
即有f(x)=ex-2x的导数为f′(x)=ex-2,
当x>ln2时,f′(x)>0,f(x)递增;
当x<ln2时,f′(x)<0,f(x)递减.
即有x=ln2处取得极小值,且为2-2ln2,无极大值;
(2)关于x的方程f(x)=x2-mx仅有1解,即为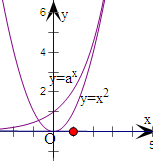
ax=x2(a>1)仅有1解.
当x<0时,函数y=ax与函数y=x2图象恒有一个交点;
由题意x>0没有交点,即ax>x2(a>1)在x>0恒成立,
设y=ax与函数y=x2图象相切的切点为(m,n),
则am=m2,且amlna=2m,
解得a=${e}^{\frac{2}{e}}$,m=e.
即有ax>x2(a>1)在x>0恒成立时,a>${e}^{\frac{2}{e}}$.
则实数a的取值范围是(${e}^{\frac{2}{e}}$,+∞).
点评 本题考查导数的运用:求切线的斜率和单调区间、极值,考查函数方程的转化思想以及数形结合的思想方法,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -200 | B. | -100 | C. | 200 | D. | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
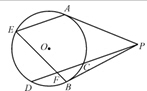 过圆O外一点P向圆引两条切线PA、PB和割线PCD,从A点作弦AE平行于CD,连接BE交CD于F.
过圆O外一点P向圆引两条切线PA、PB和割线PCD,从A点作弦AE平行于CD,连接BE交CD于F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com