
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
分析 求$\overrightarrow{a}$与$\overrightarrow{b}$的夹角,需求$\overrightarrow{a}$与$\overrightarrow{b}$的数量积的值,又由$\overrightarrow{c}$=$\overrightarrow{a}$+$\overrightarrow{b}$,且知道$\overrightarrow{c}$⊥$\overrightarrow{a}$,故可将$\overrightarrow{b}$转化为$\overrightarrow{a},\overrightarrow{c}$表示,代入进行线性运算即可.也可以利用向量的几何意义,结合图象解三角形.解题时,应注意向量$\overrightarrow{a}$ 与$\overrightarrow{b}$ 的夹角范围.
解答  解法一:
解法一:
解:∵$\overrightarrow{c}=\overrightarrow{a}+\overrightarrow{b}$
∴$\overrightarrow{b}=\overrightarrow{c}-\overrightarrow{a}$
∴$\overrightarrow{a}•\overrightarrow{b}=\overrightarrow{a}•(\overrightarrow{c}-\overrightarrow{a})$=$\overrightarrow{a}•\overrightarrow{c}-{\overrightarrow{a}}^{2}$
∵$\overrightarrow{c}⊥\overrightarrow{a}$
∴$\overrightarrow{a}•\overrightarrow{c}=0$
又 $|\overrightarrow{a}|=2$,$|\overrightarrow{b}|=4$
∴$\overrightarrow{a}•\overrightarrow{b}=-4$
∴$\overrightarrow{a}•\overrightarrow{b}=|\overrightarrow{a}|×|\overrightarrow{b}|×cos<\overrightarrow{a},\overrightarrow{b}>$=-4
∴$cos<\overrightarrow{a},\overrightarrow{b}>=-\frac{1}{2}$<0 且$<\overrightarrow{a},\overrightarrow{b}>∈[0°,180°]$
∴$<\overrightarrow{a},\overrightarrow{b}>=120°$即$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为120°.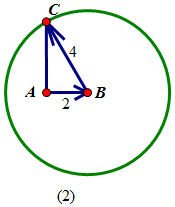
故选D.
解法二:数形结合
记$\overrightarrow{a}=\overrightarrow{AB}$,$\overrightarrow{b}=\overrightarrow{BC}$,则$|\overrightarrow{AB}|=2,|\overrightarrow{BC}|=4$
∴$\overrightarrow{c}=\overrightarrow{a}+\overrightarrow{b}$=$\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$
由于题中需求的向量$\overrightarrow{a}和\overrightarrow{b}的夹角未知$.
故可将$\overrightarrow{a}$固定,$\overrightarrow{b}$的终点C则是以点B为原点,以4为半径的圆上的动点,如上图所示.
又∵$\overrightarrow{c}⊥\overrightarrow{a}$
∴点C运动至图(2)处,满足 $\overrightarrow{c}⊥\overrightarrow{a}$
此时,△ABC是以∠A=90°的直角三角形,且|AB|=2,|BC|=4
∴∠ABC=60°
故向量$\overrightarrow{a}与\overrightarrow{b}$的夹角是∠ABC的补角,即向量$\overrightarrow{a}与\overrightarrow{b}$的夹角是120°
故选D.
点评 主要考查向量的夹角公式,向量的数量积基本运算.考查了向量的线性运算.考查了代入法,数形结合思想.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | {-2,-1} | C. | {0,1,2} | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\sqrt{5}$+3 | C. | 7-$\sqrt{5}$ | D. | 7+$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 38% | B. | 76% | C. | 90% | D. | 95% |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com