考点:利用导数研究函数的极值,利用导数求闭区间上函数的最值
专题:综合题,导数的综合应用
分析:(Ⅰ)求导数,利用函数f(x)=(x
2+ax)e
x在(-∞,0)上有且仅有一个极值点x
0,可得f'(0)=a<0;
(Ⅱ)(ⅰ)令f'(x)=0,求出x
0,即可证明;
(ⅱ)M=f(x
0)-g(0)=f(x
0)-a,进而可得M=f(x
0)-a=
-•ex0+
,求导,确定单调性,即可得出结论.
解答:
(Ⅰ)解:∵f(x)=(x
2+ax)e
x∴f'(x)=[x
2+(a+2)x-2a]e
x,
∵函数f(x)=(x
2+ax)e
x在(-∞,0)上有且仅有一个极值点x
0.
∴f'(0)=a<0;
(Ⅱ)(ⅰ)证明:令f'(x)=0,则
a<0时,x
0=
=-1-
,
∵a<0,∴0<
<1
∴-2<-1-
<-1
∴-2<x
0<-1;
(ⅱ)解:a<0时,函数f(x)=(x
2+ax)e
x在(-∞,0)上有且仅有一个极值点x
0.
f(x)=(x
2+ax)e
x>0在(-∞,0)上恒成立,故f(x
1)∈(0,f(x
0)],
且g(x)=
在[0,+∞)上单调递增,故g(x
2)∈[g(0),0),
∴M=f(x
0)-g(0)=f(x
0)-a.
由f'(x
0)=0,可得a=-
,
∴f(x
0)=
-•ex0,
∴M=f(x
0)-a=
-•ex0+
,
令h(x
0)=
-•ex0+
(-2<x
0<-1)
则h′(x
0)=
•ex0+
>0
∴h(x
0)>h(-2)=
,
∴M>
.
点评:本题考查导数知识的综合运用,考查函数的极值,考查恒成立问题,考查学生分析解决问题的能力,属于中档题.



 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案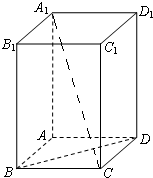 如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,连接A1C,BD.
如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,连接A1C,BD.