解:(I)函数f(x)的定义域为(0,+∞),
∵f(x)=x+
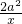
+alnx,∴f′(x)=1-
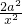
+

=
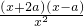
,
当a=0时,f′(x)=1>0,所以f(x)的单调递增区间是(0,+∞);
当a>0时,由f′(x)>0,即
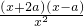
>0,解得x>a,所以f(x)的单调递增区间是(a,+∞);
当a<0时,由f′(x)>0,即
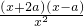
>0,解得x>-2a,所以f(x)的单调递增区间是(-2a,+∞).
(II)当a=1时,g(x)=1-

+

,假设存在实数k,使得g(x)的图象上任意不同两点连线的斜率都不小于k,
即对任意x
2>x
1>0,都有
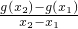
≥k,亦即g(x
2)-kx
2≥g(x
1)-kx
1,
可设函数h(x)=g(x)-kx=1-

+

-kx(x>0),
故问题等价于h′(x)=
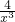
-

-k≥0,即k≤
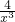
-

对x>0恒成立,
令t=

,则F(t)=4t
3-t
2(t>0),所以F′(t)=12t
2-2t,
令F′(t)=0,解得t=0(舍去)或t=

,
当t变化时,F(t)与F′(t)的变化情况如下表:

故知F(t)在(0,

)内单调递减,在(

,+∞)内单调递增,
所以当t=

时,F(t)取得最小值,且最小值为-
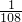
,
∴当x>0时,F(

)=
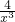
-

≥-
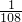
,当且仅当x=6时取等号,
故k的取值范围是(-∞,-
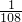
].
分析:(I)根据负数没有对数求出f(x)的定义域,然后求出f(x)的导函数,分a=0,a大于0和a小于0三种情况令导函数大于0,求出相应的x的解,即可单调f(x)的单调递增区间;
(II)把a=1代入f(x)的导函数确定出g(x),假设存在实数k,使得g(x)的图象上任意不同两点连线的斜率都不小于k,可设在定义域内任意的两个自变量x,利用斜率的计算方法表示出斜率,并大于等于k,去分母变形,然后设h(x)=g(x)-kx,求出h(x)的导函数,解出k小于等于一个函数恒成立,令t=

,设这个函数为F(t),求出F(t)的导函数,令导函数等于0,求出相应的t的值,在定义域内由t的值讨论导函数的正负进而得到函数的单调区间,根据函数的增减性得到函数的最小值,让k小于等于求出的最小值即可得到k的取值范围.
点评:本题考查函数、导数等基础知识,考查了推理论证能力、运算求解能力、创新意识,考查了函数与方程的思想、化归与转化思想、分类与整合思想及有限与无限思想,是一道中档题.

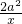 +alnx.
+alnx.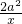 +alnx,∴f′(x)=1-
+alnx,∴f′(x)=1-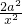 +
+ =
=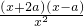 ,
,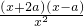 >0,解得x>a,所以f(x)的单调递增区间是(a,+∞);
>0,解得x>a,所以f(x)的单调递增区间是(a,+∞);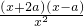 >0,解得x>-2a,所以f(x)的单调递增区间是(-2a,+∞).
>0,解得x>-2a,所以f(x)的单调递增区间是(-2a,+∞). +
+ ,假设存在实数k,使得g(x)的图象上任意不同两点连线的斜率都不小于k,
,假设存在实数k,使得g(x)的图象上任意不同两点连线的斜率都不小于k,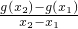 ≥k,亦即g(x2)-kx2≥g(x1)-kx1,
≥k,亦即g(x2)-kx2≥g(x1)-kx1, +
+ -kx(x>0),
-kx(x>0),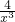 -
- -k≥0,即k≤
-k≥0,即k≤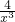 -
- 对x>0恒成立,
对x>0恒成立, ,则F(t)=4t3-t2(t>0),所以F′(t)=12t2-2t,
,则F(t)=4t3-t2(t>0),所以F′(t)=12t2-2t, ,
,
 )内单调递减,在(
)内单调递减,在( ,+∞)内单调递增,
,+∞)内单调递增, 时,F(t)取得最小值,且最小值为-
时,F(t)取得最小值,且最小值为-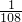 ,
, )=
)=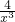 -
- ≥-
≥-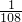 ,当且仅当x=6时取等号,
,当且仅当x=6时取等号,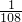 ].
]. ,设这个函数为F(t),求出F(t)的导函数,令导函数等于0,求出相应的t的值,在定义域内由t的值讨论导函数的正负进而得到函数的单调区间,根据函数的增减性得到函数的最小值,让k小于等于求出的最小值即可得到k的取值范围.
,设这个函数为F(t),求出F(t)的导函数,令导函数等于0,求出相应的t的值,在定义域内由t的值讨论导函数的正负进而得到函数的单调区间,根据函数的增减性得到函数的最小值,让k小于等于求出的最小值即可得到k的取值范围.

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<