(Ⅰ)解:由f(x)=xlnx+ax,得:f
′(x)=lnx+a+1
∵函数f(x)在区间[e
2,+∞)上为增函数,
∴当x∈[e
2,+∞)时f
′(x)≥0,
即lnx+a+1≥0在区间[e
2,+∞)上恒成立,
∴a≥-1-lnx.
又当x∈[e
2,+∞)时,
lnx∈[2,+∞),∴-1-lnx∈(-∞,-3].
∴a≥-3;
(Ⅱ)若对任意x∈(1,+∞),f(x)>k(x-1)+ax-x恒成立,
即x•lnx+ax>k(x-1)+ax-x恒成立,
也就是k(x-1)<x•lnx+ax-ax+x恒成立,
∵x∈(1,+∞),∴x-1>0.
则问题转化为k

对任意x∈(1,+∞)恒成立,
设函数h(x)=
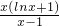
,则
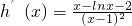
,
再设m(x)=x-lnx-2,则

.
∵x∈(1,+∞),∴m
′(x)>0,则m(x)=x-lnx-2在(1,+∞)上为增函数,
∵m(1)=1-ln1-2=-1,m(2)=2-ln2-2=-ln2,m(3)=3-ln3-2=1-ln3<0,m(4)=4-ln4-2=2-ln4>0.
∴?x
0∈(3,4),使m(x
0)=x
0-lnx
0-2=0.
∴当x∈(1,x
0)时,m(x)<0,h
′(x)<0,∴
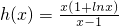
在(1,x
0)上递减,
x∈(x
0,+∞)时,m(x)>0,h
′(x)>0,∴
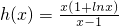
在(x
0,+∞)上递增,
∴h(x)的最小值为h(x
0)=
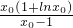
.
∵m(x
0)=x
0-lnx
0-2=0,∴lnx
0+1=x
0-1,代入函数h(x)=
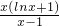
得h(x
0)=x
0,
∵x
0∈(3,4),且k<h(x)对任意x∈(1,+∞)恒成立,
∴k<h(x)
min=x
0,∴k≤3,
∴k的值为1,2,3.
分析:(Ⅰ)求出原函数的导函数,由函数f(x)在区间[e
2,+∞)上为增函数,得其导函数在[e
2,+∞)上大于等于0恒成立,把变量a分离出后得a≥-1-lnx,然后利用函数的单调性求-1-lnx在[e
2,+∞)上的最大值,答案可求;
(Ⅱ)把函数f(x)的解析式代入f(x)>k(x-1)+ax-x,整理后得k

,问题转化为对任意
x∈(1,+∞),k

恒成立,求正整数k的值.设函数h(x)=
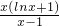
,求其导函数,得到其导函数的零点x
0位于(3,4)内,且知此零点为函数h(x)的最小值点,经求解知h(x
0)=x
0,从而得到k<x
0,则正整数k的值可求.
点评:本题考查了利用导数研究函数的单调性,考查了导数在最大值和最小值中的应用,考查了数学转化思想,解答此题的关键是,在求解(Ⅱ)时如何求解函数h(x)=
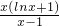
的最小值,学生思考起来有一定难度.此题属于难度较大的题目.

 对任意x∈(1,+∞)恒成立,
对任意x∈(1,+∞)恒成立,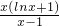 ,则
,则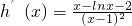 ,
, .
.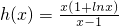 在(1,x0)上递减,
在(1,x0)上递减,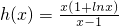 在(x0,+∞)上递增,
在(x0,+∞)上递增,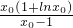 .
.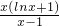 得h(x0)=x0,
得h(x0)=x0, ,问题转化为对任意
,问题转化为对任意 恒成立,求正整数k的值.设函数h(x)=
恒成立,求正整数k的值.设函数h(x)=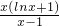 ,求其导函数,得到其导函数的零点x0位于(3,4)内,且知此零点为函数h(x)的最小值点,经求解知h(x0)=x0,从而得到k<x0,则正整数k的值可求.
,求其导函数,得到其导函数的零点x0位于(3,4)内,且知此零点为函数h(x)的最小值点,经求解知h(x0)=x0,从而得到k<x0,则正整数k的值可求.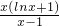 的最小值,学生思考起来有一定难度.此题属于难度较大的题目.
的最小值,学生思考起来有一定难度.此题属于难度较大的题目. 

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<