
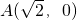 ,
,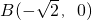 ,直线PA与PB的斜率之积为
,直线PA与PB的斜率之积为 .
. …(2分)
…(2分) …(4分)
…(4分) 整理得(m2+2)y2+2my-1=0…(6分)
整理得(m2+2)y2+2my-1=0…(6分)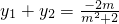 ,
,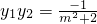 ,…(8分)
,…(8分)
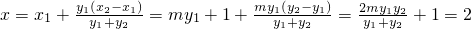 …(10分)
…(10分) 整理得(1+2k2)x2-4k2x+2k2-2=0…(6分)
整理得(1+2k2)x2-4k2x+2k2-2=0…(6分)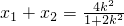 ,
, ,…(8分)
,…(8分)
 …(10分)
…(10分) ,建立等式,化简,即可求得求动点P轨迹E的方程;
,建立等式,化简,即可求得求动点P轨迹E的方程;

 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:
| π | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| 3π |
| 2 |
| AC |
| BC |
| π |
| 2 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com