
| A. | 1 | B. | 2 | C. | 3 | D. | 5 |
分析 把点A(1,2)代入抛物线Γ:y2=2px上,可得p=2.即可得到抛物线Γ的方程为:y2=4x.设B($\frac{{y}_{1}^{2}}{4}$,y1),C($\frac{{y}_{2}^{2}}{4}$,y2),分别求得k1,k2,k3,代入即可求得$\frac{1}{k_1}-\frac{1}{k_2}+\frac{1}{k_3}$的值.
解答 解:(1)∵点A(1,2)在抛物线Γ:y2=2px上,∴22=2p×1,解得p=2.
∴抛物线Γ的方程为:y2=4x.
设B($\frac{{y}_{1}^{2}}{4}$,y1),C($\frac{{y}_{2}^{2}}{4}$,y2),
k1=$\frac{{y}_{1}-2}{\frac{{y}_{1}^{2}}{4}-1}$=$\frac{4}{{y}_{1}+2}$,k2=$\frac{{y}_{1}-{y}_{2}}{\frac{{y}_{1}^{2}}{4}-\frac{{y}_{2}^{2}}{4}}$=$\frac{4}{{y}_{1}+{y}_{2}}$,k3=$\frac{{y}_{2}-2}{\frac{{y}_{2}^{2}}{4}-1}$=$\frac{4}{{y}_{2}+2}$,
$\frac{1}{k_1}-\frac{1}{k_2}+\frac{1}{k_3}$=$\frac{{y}_{1}+2}{4}$-$\frac{{y}_{1}+{y}_{2}}{4}$+$\frac{{y}_{2}+2}{4}$=1,
故选:A.
点评 本题考查了抛物线的标准方程及其性质、斜率计算公式,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 10与4 | B. | 10与2 | C. | 4与10 | D. | 2与10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-2)2+(y+1)2=4 | B. | (x+2)2+(y-1)2=4 | C. | (x-2)2+(y+1)2=16 | D. | (x+2)2+(y-1)2=16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
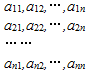 设A1,A2,…,An(n≥4)为集合S={1,2,…,n}的n个不同子集,为了表示这些子集,作n行n列的数阵,规定第i行第j列的数为:${a_{ij}}=\left\{\begin{array}{l}0,\;i∉{A_j}\\ 1,\;i∈{A_j}\end{array}\right.$.则下列说法中,错误的是( )
设A1,A2,…,An(n≥4)为集合S={1,2,…,n}的n个不同子集,为了表示这些子集,作n行n列的数阵,规定第i行第j列的数为:${a_{ij}}=\left\{\begin{array}{l}0,\;i∉{A_j}\\ 1,\;i∈{A_j}\end{array}\right.$.则下列说法中,错误的是( )| A. | 数阵中第一列的数全是0当且仅当A1=∅ | |
| B. | 数阵中第n列的数全是1当且仅当An=S | |
| C. | 数阵中第j行的数字和表明集合Aj含有几个元素 | |
| D. | 数阵中所有的n2个数字之和不超过n2-n+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | cos70° | D. | sin70° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com