
分析 运用等差数列的求和公式,可得a1+a2+…+an,再将bn写成$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$),运用裂项相消求和,即可得到结论.
解答 解:由an=2n+1,可得
a1+a2+…+an=$\frac{1}{2}$n(3+2n+1)=n(n+2),
则bn=$\frac{1}{{a}_{1}+{a}_{2}+…+{a}_{n}}$
=$\frac{1}{n(n+2)}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$),
即有数列{bn}的前n项和为
Sn=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{2}$-$\frac{1}{4}$+…+$\frac{1}{n-1}$-$\frac{1}{n+1}$+$\frac{1}{n}$-$\frac{1}{n+2}$)
=$\frac{1}{2}$(1+$\frac{1}{2}$-$\frac{1}{n+1}$-$\frac{1}{n+2}$)
=$\frac{1}{2}$($\frac{3}{2}$-$\frac{1}{n+1}$-$\frac{1}{n+2}$).
故答案为:$\frac{1}{2}$($\frac{3}{2}$-$\frac{1}{n+1}$-$\frac{1}{n+2}$).
点评 本题考查等差数列的通项和求和公式的运用,同时考查数列的求和方法:裂项相消求和,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
| 认为作业多 | 认为作业不多 | |
| 喜欢玩手机 | 18 | 9 |
| 不喜欢玩手机 | 7 | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x($\frac{1}{2}$)x | B. | y=-($\frac{1}{2}$)x | C. | y=xlog2x | D. | y=x${\;}^{\frac{1}{3}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在第十六届广州亚运会上,某项目的比赛规则为:由两人(记为甲和乙)进行比赛,每局胜者得1分,负者得0分(无平局),比赛进行到有一人比对方多2分或打满6局时停止.设甲在每局中获胜的概率为p(p>0.5),且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为$\frac{5}{9}$.
在第十六届广州亚运会上,某项目的比赛规则为:由两人(记为甲和乙)进行比赛,每局胜者得1分,负者得0分(无平局),比赛进行到有一人比对方多2分或打满6局时停止.设甲在每局中获胜的概率为p(p>0.5),且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为$\frac{5}{9}$.查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽六安一中高二上理周末检测三数学试卷(解析版) 题型:选择题
若数列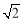 ,
, ,
, ,
, ,
, ,……,则
,……,则 是这个数列的第( )项
是这个数列的第( )项
A.8 B.9 C.10 D.11
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com