练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知非空集合A={x|a＜x＜2a+3}，B={x|0＜x＜1}
    （1）若a=﹣ ，求 A∩B
    （2）若A∩B=，求实数a的取值范围．

    【答案】
    （1）解：把a=﹣ 代入得：A={x|﹣ ＜x＜2}，

    ∵B={x|0＜x＜1}，

    ∴A∩B={x|0＜x＜1}


    （2）解：∵A∩B=，

    ∴A=或2a+3≤0或a≥1，

    解得：a≤﹣3或a≤﹣ 或a≥1，

    则a的范围是a≤﹣ 或a≥1


    【解析】（1）把a的值代入确定出A，求出A与B的交集即可；（2）根据A与B的交集为空集，确定出a的范围即可．
    【考点精析】利用集合的交集运算对题目进行判断即可得到答案，需要熟知交集的性质：（1）A∩BA，A∩BB，A∩A=A，A∩=,A∩B=B∩A;（2）若A∩B=A，则AB，反之也成立．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数g（x）=x2﹣ax+b，其图象对称轴为直线x=2，且g（x）的最小值为﹣1，设f（x）= ．
    （1）求实数a，b的值；
    （2）若不等式f（3x）﹣t3x≥0在x∈[﹣2，2]上恒成立，求实数t的取值范围；
    （3）若关于x的方程f（|2x﹣2|）+k ﹣3k=0有三个不同的实数解，求实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x2+2ax+2，x∈[﹣5，5]．
    （1）当a=﹣1时，求函数f（x）的最大值和最小值；
    （2）当a∈R时，求函数f（x）的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列命题：
    ①函数y=﹣ 在其定义域上是增函数；
    ②函数y= 是奇函数；
    ③函数y=log2（x﹣1）的图象可由y=log2（x+1）的图象向右平移2个单位得到；
    ④若（ ）a=（ ）b＜1．则a＜b＜0
    则下列正确命题的序号是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，内角A，B，C所对的边分别为a，b，c．已知a﹣c= b，sinB= sinC．
    （1）求cosA的值；
    （2）求cos（A+ ）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}满足an=3an﹣1+3n﹣1（n∈N*，n≥2）且a3=95．
    （1）求a1 ， a2的值；
    （2）求实数t，使得bn= （an+t）（n∈N*）且{bn}为等差数列；
    （3）在（2）条件下求数列{an}的前n项和Sn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设命题p：函数y=kx+1在R上是增函数，命题q：x∈R，x2+（2k﹣3）x+1=0，如果p∧q是假命题，p∨q是真命题，求k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=2﹣ （x＞0），若存在实数m、n（m＜n）使f（x）在区间（m，n）上的值域为（tm，tn），则实数t的取值范围是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

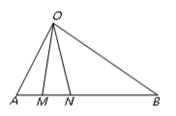
    【题目】如图所示，某公路 一侧有一块空地 ，其中 ， ．当地政府拟在中间开挖一个人工湖△OMN，其中M，N都在边AB上（M，N不与A，B重合，M在A，N之间），且∠MON＝30°．

    （1）若M在距离A点2 km处，求点M，N之间的距离；

    （2）为节省投入资金，人工湖△OMN的面积要尽可能小．试确定M的位置，使△OMN的面积最小，并求出最小面积．

    查看答案和解析>>

    同步练习册答案