
| A. | -2 | B. | 1 | C. | -2或1 | D. | m的值不存在 |
分析 根据题意,由向量平行的坐标表示可得m×(m+1)=2×1,解可得m的值,将m的值代入$\overrightarrow a$、$\overrightarrow b$的坐标,验证$\overrightarrow a$与$\overrightarrow b$是否反向,即可得答案.
解答 解:向量$\overrightarrow a=({m,2}),\overrightarrow b=({1,m+1})$,
若$\overrightarrow a$∥$\overrightarrow b$,则有m×(m+1)=2×1,
解可得m=-2或1;
当m=1时,$\overrightarrow a=({1,2}),\overrightarrow b=({1,2})$,$\overrightarrow a$与$\overrightarrow b$的方向相同,舍去;
当m=-2时,$\overrightarrow a=({-2,2}),\overrightarrow b=({1,-1})$,$\overrightarrow a$与$\overrightarrow b$的方向相反,符合题意;
故选:A.
点评 本题考查向量共线的坐标表示,关键是利用向量共线的坐标表示公式,得到关于m的方程.


科目:高中数学 来源: 题型:选择题
| A. | 如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥γ | |
| B. | 如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β | |
| C. | 如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β | |
| D. | 如果平面α⊥平面β,且直线l∥平面α,则直线l⊥平面β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
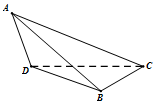 如图,在三棱锥A-BCD中,△ABD为边长等于$\sqrt{2}$正三角形,CD=CB=1.△ADC与△ABC是有公共斜边AC的全等的直角三角形.
如图,在三棱锥A-BCD中,△ABD为边长等于$\sqrt{2}$正三角形,CD=CB=1.△ADC与△ABC是有公共斜边AC的全等的直角三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30m | B. | 40m | C. | $40\sqrt{3}$m | D. | $40\sqrt{2}$m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com