
【题目】如图,正四棱锥![]() 的底面边长为
的底面边长为![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点.
的中点.
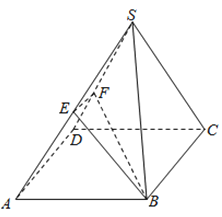
(1)当![]() 时,证明:平面
时,证明:平面![]() 平面
平面![]() ;
;
(2)若平面![]() 与底面
与底面![]() 所成锐二面角为
所成锐二面角为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)根据四棱锥是正四棱锥,连接![]() 交
交![]() 于点
于点![]() ,以
,以![]() 为原点,以
为原点,以![]() 、
、![]() 、
、![]() 建立空间坐标系.取
建立空间坐标系.取![]() 的中点
的中点![]() ,用向量法证明
,用向量法证明![]() ,
,![]() ,得到
,得到![]() 平面
平面![]() ,再用面面垂直的判定定理证明;
,再用面面垂直的判定定理证明;
(2)设![]() ,求得平面
,求得平面![]() 的一个法向量,取平面
的一个法向量,取平面![]() 的一个法向量,根据平面
的一个法向量,根据平面![]() 与底面
与底面![]() 所成锐二面角为
所成锐二面角为![]() ,由
,由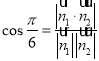 ,求得
,求得![]() ,设直线
,设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,代入公式
,代入公式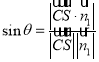 求解.
求解.
(1)连接![]() 交
交![]() 于点
于点![]() ,建立如图所示空间坐标系.
,建立如图所示空间坐标系.
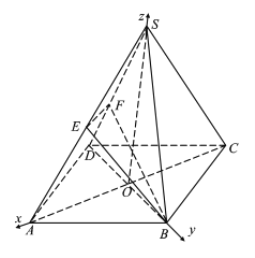
∵![]() ,∴
,∴![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,![]() ,
,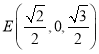 ,
,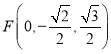 ,
,
设![]() 是
是![]() 的中点,则
的中点,则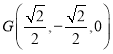 ,
,
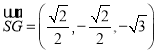 ,
,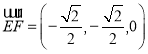 ,
,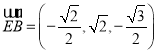 ,
,
∵![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,
![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ;
;
(2)设![]() ,则
,则![]() ,
,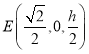 ,
,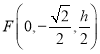 ,
,
则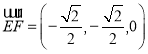 ,
,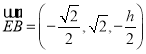 ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则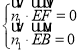 ,即
,即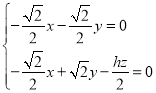 ,
,
令![]() ,则
,则![]() ,
,![]() ,所以
,所以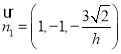 ,
,
取平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则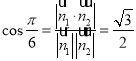 ,即
,即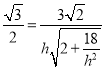 ,解得
,解得![]() ,∴
,∴![]() ,
,
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,∴
,∴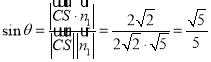 ,
,
即直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最小正周期为
的最小正周期为![]() ,其图象关于直线
,其图象关于直线![]() 对称.给出下面四个结论:①将
对称.给出下面四个结论:①将![]() 的图象向右平移
的图象向右平移![]() 个单位长度后得到函数图象关于原点对称;②点
个单位长度后得到函数图象关于原点对称;②点![]() 为
为![]() 图象的一个对称中心;③
图象的一个对称中心;③![]() ;④
;④![]() 在区间
在区间![]() 上单调递增.其中正确的结论为( )
上单调递增.其中正确的结论为( )
A.①②B.②③C.②④D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={(x,y)|(x﹣3﹣4cosq)2+(y﹣5﹣4sinq)2=4,θ∈R},B={(x,y)|3x+4y﹣19=0}.记集合P=A∩B,则集合P所表示的轨迹的长度为( )
A.8![]() B.8
B.8![]() C.8
C.8![]() D.8
D.8![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“未来肯定是非接触的,无感支付的方式将成为主流,这有助于降低交互门槛”.云从科技联合创始人姚志强告诉南方日报记者.相对于主流支付方式二维码支付,刷脸支付更加便利,以前出门一部手机解决所有,而现在连手机都不需要了,毕竟,手机支付还需要携带手机,打开二维码也需要时间和手机信号.刷脸支付将会替代手机,成为新的支付方式.某地从大型超市门口随机抽取50名顾客进行了调查,得到了如下列联表:
男性 | 女性 | 总计 | |
刷脸支付 | 18 | 25 | |
非刷脸支付 | 13 | ||
总计 | 50 |
(1)请将上面的列联表补充完整,并判断是否有95%的把握认为使用刷脸支付与性别有关?
(2)从参加调查且使用刷脸支付的顾客中随机抽取2人参加抽奖活动,抽奖活动规则如下:
“一等奖”中奖概率为0.25,奖品为10元购物券![]() 张(
张(![]() ,且
,且![]() ),“二等奖”中奖概率0.25,奖品为10元购物券两张,“三等奖”中奖概率0.5,奖品为10元购物券一张,每位顾客是否中奖相互独立,记参与抽奖的两位顾客中奖购物券金额总和为
),“二等奖”中奖概率0.25,奖品为10元购物券两张,“三等奖”中奖概率0.5,奖品为10元购物券一张,每位顾客是否中奖相互独立,记参与抽奖的两位顾客中奖购物券金额总和为![]() 元,若要使
元,若要使![]() 的均值不低于50元,求
的均值不低于50元,求![]() 的最小值.
的最小值.
附: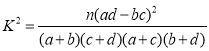 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.869 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,(其中
,(其中![]() )的图象关于点
)的图象关于点![]() 成中心对称,且与点
成中心对称,且与点![]() 相邻的一个最低点为
相邻的一个最低点为![]() ,则对于下列判断:
,则对于下列判断:
①直线![]() 是函数
是函数![]() 图象的一条对称轴;
图象的一条对称轴;
②点![]() 是函数
是函数![]() 的一个对称中心;
的一个对称中心;
③函数![]() 与
与![]() 的图象的所有交点的横坐标之和为
的图象的所有交点的横坐标之和为![]() .
.
其中所有正确的判断是( )
A.①②B.①③C.②③D.②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】1852年,英国来华传教士伟烈亚力将《孙子算经》中“物不知数”问题的解法传至欧洲.1874年,英国数学家马西森指出此法符合1801年由高斯得到的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”.“中国剩余定理”讲的是一个关于整除的问题,例如求1到2000这2000个整数中,能被3除余1且被7除余1的数的个数,现由程序框图,其中MOD函数是一个求余函数,记![]() 表示m除以n的余数,例如
表示m除以n的余数,例如![]() ,则输出i为( ).
,则输出i为( ).
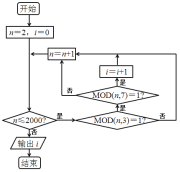
A.98B.97C.96D.95
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是椭圆
是椭圆![]() 的右焦点,过点
的右焦点,过点![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 两点,当直线
两点,当直线![]() 过
过![]() 的下顶点时,
的下顶点时,![]() 的斜率为
的斜率为![]() ,当直线
,当直线![]() 垂直于
垂直于![]() 的长轴时,
的长轴时,![]() 的面积为
的面积为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)当![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(Ⅲ)若直线![]() 上存在点
上存在点![]() 满足
满足![]() 成等比数列,且点
成等比数列,且点![]() 在椭圆外,证明:点
在椭圆外,证明:点![]() 在定直线上.
在定直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】生活中人们常用“通五经贯六艺”形容一个人才识技艺过人,这里的“六艺”其实源于中国周朝的贵族教育体系,具体包括“礼、乐、射、御、书、数”.为弘扬中国传统文化,某校在周末学生业余兴趣活动中开展了“六艺”知识讲座,每艺安排一节,连排六节,则满足“数”必须排在前两节,“礼”和“乐”必须分开安排的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com