

 ,且△ABC的面积为
,且△ABC的面积为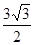 ,求a+b的值。
,求a+b的值。科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,该车的底盘与轮胎中心在同一水平面上. 该车的涉水安全要求是:水面不能超过它的底盘高度. 如图所示:某处有一“坑形”地面,其中坑
,该车的底盘与轮胎中心在同一水平面上. 该车的涉水安全要求是:水面不能超过它的底盘高度. 如图所示:某处有一“坑形”地面,其中坑 形成顶角为
形成顶角为 的等腰三角形,且
的等腰三角形,且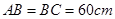 ,如果地面上有
,如果地面上有 (
( )高的积水(此时坑内全是水,其它因素忽略不计).
)高的积水(此时坑内全是水,其它因素忽略不计). 、
、 同时接触时,求证:此轮胎露在水面外的高度(从轮胎最上部到水面的距离)为
同时接触时,求证:此轮胎露在水面外的高度(从轮胎最上部到水面的距离)为 ;
; 的最大值.
的最大值.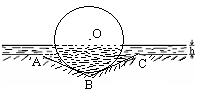
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com