
分析 (1)写出所有基本事件,求出总个数,
(2)求出三次颜色全相同的基本事件个数,代入古典概型概率公式计算;
(3)求出三次抽取的红球数多于白球数的基本事件个数,代入古典概型概率公式计算
解答 解:(1)由题意,基本事件共有23=8个结果,分别是(红,红,红),(红,红,白),(红,白,红),(白,红,红),
(红,白,白),(白,红,白),(白,白,红),(白,白,白).
(2)三次颜色全相同有2个结果,
∴三次颜色全相同的概率为$\frac{2}{8}$=$\frac{1}{4}$;
(3)三次抽取的红球数多于白球数的有4个结果,
∴三次抽取的红球数多于白球数的概率为$\frac{4}{8}$=$\frac{1}{2}$.
点评 本题考查了等可能事件的概率,如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{19}}{2}$ | B. | 2$\sqrt{19}$ | C. | $\sqrt{19}$ | D. | 8$\sqrt{19}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
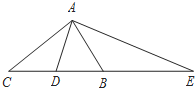 在△ABC中,∠BAC=90°,D是BC边的中点,AE⊥AD,AE交CB的延长线于E,则下面结论中正确的是( )
在△ABC中,∠BAC=90°,D是BC边的中点,AE⊥AD,AE交CB的延长线于E,则下面结论中正确的是( )| A. | △AED∽△ACB | B. | △AEB∽△ACD | C. | △BAE∽△ACE | D. | △AEC∽△DAC |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com