练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
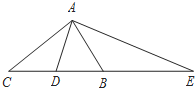
    18．在△ABC中，∠BAC=90°，D是BC边的中点，AE⊥AD，AE交CB的延长线于E，则下面结论中正确的是（　　）
    A．△AED∽△ACBB．△AEB∽△ACDC．△BAE∽△ACED．△AEC∽△DAC

    分析 先利用直角三角形斜边上的中线等于斜边的一半得到DA=DC，则∠DAC=∠C，再利用等角的余角相等得到∠EAB=∠DAC，从而有∠EAB=∠C，再加上公共角即可判断△BAE∽△ACE．

    解答 解：∵∠BAC=90°，D是BC中点，
    ∴DA=DC，
    ∴∠DAC=∠C，
    又∵AE⊥AD，
    ∴∠EAB+∠BAD=90°，∠CAD+∠BAD=90°，
    ∴∠EAB=∠DAC，
    ∴∠EAB=∠C，
    而∠E是公共角，
    ∴△BAE∽△ACE
    故选C．

    点评 此题主要考查学生对相似三角形判定定理的掌握和应用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    8．袋中有红、白色球各一个，每次任取一个，有放回地抽三次，
    （1）写出所有的基本事件；
    （2）求三次颜色全相同的概率；
    （3）求三次抽取的球中红色球出现的次数多于白色球出现的次数的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．若函数f（n）属于自然数的增函数，f[f（n）]=3n，则f（10）=19．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．6本相同的数学书和3本相同的语文书分给9个人，每人1本，共有不同分法（　　）
    A．C${\;}_{9}^{3}$B．A${\;}_{9}^{3}$C．A${\;}_{9}^{6}$D．A${\;}_{9}^{3}$•A${\;}_{3}^{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知等差数列{an}中，公差d≠0，a2是a1与a4的等比中项，且a4-a1=6，在等比数列{bn}中，公比q＞0，且b1=a1，b3=a4．
    （1）求数列{an}和{bn}的通项公式；
    （2）设Cn=$\frac{1}{2n（{a}_{n}+2）}$，数列{Cn}的前n项和为Tn．若Tn＞$\frac{1}{8}$（1-m2）对n∈N*恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．曲线y=ax2在点x=1处的切线的倾斜角不小于$\frac{π}{4}$，则a的取值范围（-∞，0）∪[$\frac{1}{2}$，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．函数y=sin2（$\frac{ω}{2}$x-$\frac{π}{4}$）（ω＞0）的最小正周期为π，则ω为（　　）
    A．2B．$\frac{1}{2}$C．4D．$\frac{1}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．某中学对高二甲、乙两个同类班级，进行“加强‘语文阅读理解’训练，对提高‘数学应用题’得分率的作用”的试验，其中甲班为试验班（加强语文阅读理解训练），乙班为对比班（常规教学，无额外训练），在试验前的测试中，甲、乙两班学生在数学应用题上的得分率基本一致，试验结束后，统计几次数学应用题测试的平均成绩（均取整数）如下表所示：
    60分以下61-70分71-80分81-90分91-100分
    甲班（人数）361118
    12乙班（人数）713101010
    现规定平均成绩在80分以上（不含80分）的为优秀．
    （I）试分析估计两个班级的优秀率；
    （Ⅱ）由以上统计数据填写下面2x2列联表，根据以上数据，能杏有95%的把握认为“加强‘语文阅读理解’训练对提高‘数学应用题’得分率”有帮助？
    优秀人数非优秀人数合计
    甲班
    乙班
    合计
    参考公式及数据：x2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
    P（x2≥k0）0.500.400.250.150.100.050.0280.0100.0050.001
    k00.4550.7081.3232.0722.7063.8415.0246.6357.87910.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．若（2+x）7=a0+a1（x+1）+a2（x+1）2+…+a7（x+1）7，则a1+a3+a5+a7等于（　　）
    A．$\frac{127}{2}$B．$\frac{255}{2}$C．64D．128

    查看答案和解析>>

    同步练习册答案