
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源:不详 题型:解答题
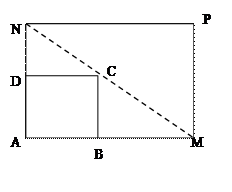 (Ⅱ)若AN的长度不小于6米,则当AM、AN的长度是多少时,矩形AMPN的面积最小并求出最小面积.
(Ⅱ)若AN的长度不小于6米,则当AM、AN的长度是多少时,矩形AMPN的面积最小并求出最小面积.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 型电脑.1993年这种电脑每台平均生产成本为5000元,并以纯利润
型电脑.1993年这种电脑每台平均生产成本为5000元,并以纯利润 确定出厂价.从1994年开始,公司通过更新设备和加强管理,使生产成本逐年降低.到1997年,尽管
确定出厂价.从1994年开始,公司通过更新设备和加强管理,使生产成本逐年降低.到1997年,尽管 型电脑出厂价仅是1993年出厂价的
型电脑出厂价仅是1993年出厂价的 ,但却实现了
,但却实现了 纯利润的高效益.
纯利润的高效益. 型电脑的生产成本;
型电脑的生产成本; ,以下数据可供参考:
,以下数据可供参考: ,
, ).
).查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

 在区间
在区间 上的最大值
上的最大值
 使得
使得 的图象与
的图象与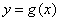 的图象有且只有三个不同的交点?若存在,求出
的图象有且只有三个不同的交点?若存在,求出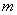 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,f2(x)=x+2,
,f2(x)=x+2, ,试画出y=f(x)的图像并求y=f(x)的曲线绕x轴旋转一周所得几何体的表面积;
,试画出y=f(x)的图像并求y=f(x)的曲线绕x轴旋转一周所得几何体的表面积; ],求b的值.
],求b的值. 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 时整,甲船自
时整,甲船自 处以
处以 的速度向正东行驶,乙船自
的速度向正东行驶,乙船自 的正北
的正北 处以
处以 的速度向正南行驶,则当日
的速度向正南行驶,则当日 时
时 分时两船之间距离对时间的变化率是_____________.
分时两船之间距离对时间的变化率是_____________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com