Question

（本题满分10分）在数列{a_n}，{b_n}中，a₁＝2，b₁＝4，且a_n，b_n，a_n＋1成等差数列，b_n，a_n＋1，b_n＋1成等比数列(n∈N^*)．求a₂，a₃，a₄及b₂，b₃，b₄，由此猜测{a_n}，{b_n}的通项公式，并证明你的结论．

 

Answer 1

【答案】

a₂＝6，b₂＝9，a₃＝12，b₃＝16，a₄＝20，b₄＝25.证明见解析.

猜测a_n＝n(n＋1)，b_n＝(n＋1)²，n∈N^*.     

【解析】主要考查了数列的通项公式和数学归纳法的运用。

由条件得2b_n＝a_n＋a_n＋1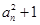，＝b_nb_n＋1，

由此可得a₂＝6，b₂＝9，a₃＝12，b₃＝16，a₄＝20，b₄＝25.

猜测a_n＝n(n＋1)，b_n＝(n＋1)²，n∈N^*.

用数学归纳法证明：

①当n＝1时，由已知a₁＝2，b₁＝4可得结论成立．

②假设当n＝k(k≥2且k∈N^*)时，结论成立，即

a_k＝k(k＋1)，b_k＝(k＋1)²，

那么当n＝k＋1时，

a_k＋1＝2b_k－a_k＝2(k＋1)²－k(k＋1)＝(k＋1)(k＋2)，

b_k＋1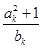＝＝＝(k＋2)².

解：由条件得2b_n＝a_n＋a_n＋1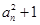，＝b_nb_n＋1，

由此可得a₂＝6，b₂＝9，a₃＝12，b₃＝16，a₄＝20，b₄＝25.

猜测a_n＝n(n＋1)，b_n＝(n＋1)²，n∈N^*.                     4分

用数学归纳法证明：

①当n＝1时，由已知a₁＝2，b₁＝4可得结论成立．

②假设当n＝k(k≥2且k∈N^*)时，结论成立，即

a_k＝k(k＋1)，b_k＝(k＋1)²，

那么当n＝k＋1时，

a_k＋1＝2b_k－a_k＝2(k＋1)²－k(k＋1)＝(k＋1)(k＋2)，

b_k＋1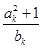＝＝＝(k＋2)².

所以当n＝k＋1时，结论也成立．

由①②可知，a_n＝n(n＋1)，b_n＝(n＋1)²对一切n∈N^*都成立．     10分