
分析 点P(1,1)在圆x2+y2=9内,弦|AB|的最大值是直径,再求出|AB|的最小值,由此能求出弦|AB|的最大值与最小值的积.
解答 解:∵12+12<9,
∴点P(1,1)在圆x2+y2=9内,
∵过点P(1,1)作直线l与圆x2+y2=9分别相交于A,B两点,
∴弦|AB|的最大值|AB|max=2r=6,
|OP|=$\sqrt{1+1}=\sqrt{2}$,r=3,
弦|AB|的最小值|AB|min=2$\sqrt{{r}^{2}-|OP{|}^{2}}$=$\sqrt{9-2}$=2$\sqrt{7}$,
∴弦|AB|的最大值与最小值的积为:6×$2\sqrt{7}$=12$\sqrt{7}$.
故答案为:12$\sqrt{7}$.
点评 本题考查弦|AB|的最大值与最小值的积的求法,是中档题,解题时要认真审题,注意圆的性质的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 2 | 3 | 4 | 5 | 6 | 7 | … |
| 3 | 5 | 7 | 9 | 11 | 13 | … |
| 4 | 7 | 10 | 13 | 16 | 19 | … |
| 5 | 9 | 13 | 17 | 21 | 25 | … |
| 6 | 11 | 16 | 21 | 26 | 31 | … |
| 7 | 13 | 19 | 25 | 31 | 37 | … |
| … | … | … | … | … | … | … |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
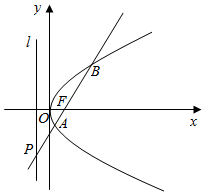 已知抛物线C:y2=2px(p>0),其焦点为F(1,0),过F作斜率为k的直线交抛物线C于A、B两点,交其准线于P点.
已知抛物线C:y2=2px(p>0),其焦点为F(1,0),过F作斜率为k的直线交抛物线C于A、B两点,交其准线于P点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com