练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．二次函数f（x）=ax2+bx+c的图象与x轴有两个交点，它们之间的距离为6，二次函数图象的对称轴方程为x=2，且f（x）有最小值为-9，求a，b，c的值．

    分析 根据已知构造关于a，b，c的方程组，解得答案．

    解答 解：∵二次函数f（x）=ax2+bx+c图象的对称轴方程为x=2，且f（x）有最小值为-9，
    且函数f（x）=ax2+bx+c的图象与x轴有两个交点，它们之间的距离为6，
    ∴$\left\{\begin{array}{l}a＞0\\-\frac{b}{2a}=2\\ \frac{4ac-{b}^{2}}{4a}=-9\\ \frac{\sqrt{{b}^{2}-4ac}}{a}=6\end{array}\right.$，
    解得：$\left\{\begin{array}{l}a=1\\ b=-4\\ c=-5\end{array}\right.$

    点评 本题考查的知识点是二次函数的图象和性质，熟练掌握二次函数的图象和性质，是解答的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    4．设实数a，b满足0≤a，b≤8，且b2=16+a2，则b-a的最大值与最小值之和为12-4$\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．今年我校高中部在全市初三学生中进行自主招生试点，通过面试招录35名优秀初三毕业生，第一轮面试共有从易到难的A、B、C、D四个问题，规则如下：
    （1）每位参加者都必须按问题A、B、C、D顺序作答，直至答题结束；
    （2）每位参加者计分器的初始分数都是100分，答对问题A加10分，答对问题B加20分，答对问题C加30分，答对问题D加60分，答错任意一题减20分；
    （3）每回答一题，计分器显示累计分数，当累计分数小于80分时，答题结束，直接淘汰出局；
    （4）当累计分数大于或等于140分时，答题结束，直接进入下一轮；
    （5）当答完四题，累计分数仍不足140分时，答题结束，淘汰出局．
    现有某学生甲对问题A、B、C、D答对的概率分别为$\frac{3}{4}$、$\frac{1}{2}$、$\frac{1}{3}$、$\frac{1}{4}$，且各题回答正确与否相互之间没有影响．
    （Ⅰ）求甲同学能进入下一轮的概率；
    （Ⅱ）用ξ表示甲同学本轮答题结束时答题的个数，求ξ的分布列和数学期望（均值）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知等差数列{an}的前n项和为Sn，公差d=2，S10=120．
    （1）求数列{an}的通项公式an；
    （2）若${b_n}={\sqrt{3}^{{a_n}-1}}$，求数列{bn}的前n项和为Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．如图1，已知四边形ABFD为直角梯形，$AB∥DF，∠ADF=\frac{π}{2}，△ADE$为等边三角形，AD=DF=2AF=2，C为DF的质点，如图2，将平面AED、BCF分别沿AD、BC折起，使得平面AED⊥平面ABCD，平面BCF⊥平面ABCD，连接EF、DF，设G为AE上任意一点．
    （1）证明：DG∥平面BCF；
    （2）求折起后的各平面围成的几何体的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

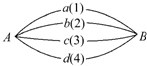    19．如图，从A地到B地设置了4条不同的网络线路，它们通过的最大信息量分别为1，2，3，4，现从中任取三条网线连通A，B两地（三条网线可通过的信息总量即三条网线各自的最大信息量之和）．
    （1）设三条网线可通过的最大信息总量为x，已知当x≥7时，可保证线路信息畅通，求线路信息畅通的概率．
    （2）为保证网络在x≥7时信息畅通的概率超过0.85，需要增加一条最大信息量为n（n≥3，n∈N）的网线与原有4条线路并联，问满足条件的n的最小值是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．直线y=x+m与椭圆$\frac{{x}^{2}}{144}$+$\frac{{y}^{2}}{25}$=1有两个公共点，则m的取值范围是（　　）
    A．（-5，5）B．（-12，12）C．（-13，13）D．（-15，15）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．已知实数x，y满足$\left\{\begin{array}{l}{x≥1}\\{x+y≤4}\\{ax+by+c≥0}\end{array}\right.$，且目标函数z=2x+y的最大值为7，最小值为1，则$\frac{4y-\frac{c}{a}}{x+\frac{c}{b}}$的取值范围是（　　）
    A．[-$\frac{1}{3}$，$\frac{10}{3}$]B．[-$\frac{1}{3}$，$\frac{8}{3}$]C．[-$\frac{2}{3}$，$\frac{14}{3}$]D．[-$\frac{2}{3}$，3]

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知函数f（x）满足f（2x-3）=4x2+2x+1．
    （1）求f（x）的解析式；
    （2）设g（x）=f（x+a）-7x，a∈R，试求g（x）在[1，3]上的最小值．

    查看答案和解析>>

    同步练习册答案