
【题目】已知![]() ,
, ![]() ,曲线
,曲线![]() 上的任意一点
上的任意一点![]() 满足:
满足: ![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)过点![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() ,
, ![]() 两点,交
两点,交![]() 轴于
轴于![]() 点,设
点,设![]() ,
, ![]() ,试问
,试问![]() 是否为定值?如果是定值,请求出这个定值,如果不是定值,请说明理由.
是否为定值?如果是定值,请求出这个定值,如果不是定值,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(Ⅰ)求出向量的坐标,利用条件化简,即可求点![]() 的轨迹方程;
的轨迹方程;
(Ⅱ)分类讨论,利用![]() ,
, ![]() ,结合韦达定理,即可得出结论.
,结合韦达定理,即可得出结论.
试题解析:(1)设![]() ,则
,则![]() ,
, ![]() ,
, ![]() ,
,
∵![]() ,∴
,∴![]() ,
,
化简得, ![]() 为所求点
为所求点![]() 的轨迹方程.
的轨迹方程.
(2)设![]() ,
, ![]() .
.
①当直线![]() 与
与![]() 轴不重合时,设直线
轴不重合时,设直线![]() 的方程为
的方程为![]() ,
,
则![]() ,从而
,从而![]() ,
, ![]() ,由
,由![]() 得
得
![]() ,
, ![]() ,
, ![]() ,
,
同理由![]() 得
得![]() ,
,
∴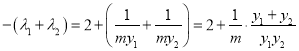 .①
.①
由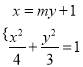 ,得
,得![]() .
.
∴![]() ,
, ![]() ,
,
代入①式得![]() ,∴
,∴![]() .
.
②当直线![]() 与
与![]() 轴重合时,
轴重合时, ![]() ,
, ![]() ,
, ![]() .
.
由![]() ,
, ![]() ,得
,得![]() ,
, ![]() ,∴
,∴![]() ,
,
综上, ![]() 为定值
为定值![]() .
.
点睛:定点、定值问题通常是通过设参数或取特殊值来确定“定点”是什么、“定值”是多少,或者将该问题涉及的几何式转化为代数式或三角问题,证明该式是恒定的. 定点、定值问题同证明问题类似,在求定点、定值之前已知该值的结果,因此求解时应设参数,运用推理,到最后必定参数统消,定点、定值显现.


科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)a的值为多少时,f(x)是偶函数?
(2)若对任意x∈[0,+∞),都有f(x)>0,求实数a的取值范围.
(3)若f(x)在区间[0,+∞)上单调递增,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把下列各命题作为原命题,分别写出它们的逆命题、否命题和逆否命题.
(1)若α=β,则sin α=sin β;
(2)若对角线相等,则梯形为等腰梯形;
(3)已知a,b,c,d都是实数,若a=b,c=d,则a+c=b+d.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在坐标原点、焦点在x轴上的椭圆,它的离心率为![]() ,且与直线x+y-1=0相交于M、N两点,若以MN为直径的圆经过坐标原点,求椭圆的方程.
,且与直线x+y-1=0相交于M、N两点,若以MN为直径的圆经过坐标原点,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在10件产品中,有3件一等品,4件二等品,3件三等品。从这10件产品中任取3件,求:
(I) 取出的3件产品中一等品件数X的分布列和数学期望;
(II) 取出的3件产品中一等品件数多于二等品件数的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个球被取出的可能性相等.
(1)求取出的两个球上标号为相同数字的概率;
(2)求取出的两个球上标号之积能被3整除的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于![]() 维向量
维向量![]() ,若对任意
,若对任意![]() 均有
均有![]() 或
或![]() ,则称
,则称![]() 为
为![]() 维
维![]() 向量. 对于两个
向量. 对于两个![]() 维
维![]() 向量
向量![]() 定义
定义![]() .
.
(1)若![]() , 求
, 求![]() 的值;
的值;
(2)现有一个![]() 维
维![]() 向量序列:
向量序列: ![]() 若
若![]() 且满足:
且满足: ![]() ,求证:该序列中不存在
,求证:该序列中不存在![]() 维
维![]() 向量
向量![]() .
.
(3) 现有一个![]() 维
维![]() 向量序列:
向量序列: ![]() 若
若![]() 且满足:
且满足: ![]() ,若存在正整数
,若存在正整数![]() 使得
使得![]() 为
为![]() 维
维![]() 向量序列中的项,求出所有的
向量序列中的项,求出所有的![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=sin2(2x﹣ ![]() )﹣2tsin(2x﹣
)﹣2tsin(2x﹣ ![]() )+t2﹣6t+1(x∈[
)+t2﹣6t+1(x∈[ ![]() ,
, ![]() ])其最小值为g(t).
])其最小值为g(t).
(1)求g(t)的表达式;
(2)当﹣ ![]() ≤t≤1时,要使关于t的方程g(t)=kt有一个实根,求实数k的取值范围.
≤t≤1时,要使关于t的方程g(t)=kt有一个实根,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com