
(08年银川一中二模理)(12分)
已知![]() =(0,-2),
=(0,-2),![]() =(0,2)其中O为坐标原点。直线L: y=-2,动点P到直线L的距离为d,且d=|
=(0,2)其中O为坐标原点。直线L: y=-2,动点P到直线L的距离为d,且d=|![]() |.
|.
(1) 求动点P的轨迹方程;
(2) 直线m: y=![]() x+1(k>0)与点P的轨迹交于M,N两点,当
x+1(k>0)与点P的轨迹交于M,N两点,当![]() 时,求直线m的倾斜角α的范围
时,求直线m的倾斜角α的范围
(3) 设直线h与点P的轨迹交于C,D两点,若![]() =-12,那么直线h一定过B点吗?请说明理由。
=-12,那么直线h一定过B点吗?请说明理由。
解析:(1)由题意知,动点P到直线L距离与到定点B的距离相等。所以P的轨迹是以B为焦点,L为准线的抛物线,其轨迹方程为x2=8y
(2)由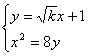 消去y得 x2-8
消去y得 x2-8![]() x-8=0, 设M(x1,y1), N(x2,y2)
x-8=0, 设M(x1,y1), N(x2,y2) ![]() =64k+32>0, k>-
=64k+32>0, k>-![]() , x1+x2=8
, x1+x2=8![]() , x1x2=-8, y1+y2=
, x1x2=-8, y1+y2=![]() x1+1+
x1+1+![]() x2+1=8k+2, y1y2=(
x2+1=8k+2, y1y2=(![]() x1+1)(
x1+1)( ![]() x2+1)=1,
x2+1)=1, ![]() =x1x2+y1y2+2(y1+y2)+4=16k+1≥17, k≥1
=x1x2+y1y2+2(y1+y2)+4=16k+1≥17, k≥1
tana≥1 且0≤a<1800 所以![]() ≤a
≤a![]() 所以的倾斜角为{a|
所以的倾斜角为{a|![]() ≤a
≤a![]() }
}
(3)设h:y=nx+b, 代入x2=8y中,得x2-8nx-8b=0. 设C(x3,y3). D(x4.y4). x3+x4=8n, x3+x4=-8b. ![]() x3x4+y3y4=b2-8b=-12, 得b=2或b=6.此时直线过点(0,2)或(0,6),故直线不一定过B点
x3x4+y3y4=b2-8b=-12, 得b=2或b=6.此时直线过点(0,2)或(0,6),故直线不一定过B点


科目:高中数学 来源: 题型:
(08年银川一中二模)(12分) 已知某几何体的三视图如下图所示,其中左视图是边长为2的正三角形,主视图是矩形且AA1=3,设D为AA1的中点。
(1)作出该几何体的直观图并求其体积;
(2)求证:平面BB1C1C⊥平面BDC1;
(3)BC边上是否存在点P,使AP//平面BDC1?若不存在,说明理由;若存在,证明你的结论。

查看答案和解析>>
科目:高中数学 来源: 题型:
(08年银川一中二模理) (12分)
设函数f(x)=(x2-x-![]() )ea x (a>0,a∈R))
)ea x (a>0,a∈R))
(1)当a=2时,求函数f(x)的单调区间
(2)若不等式f(x)+![]() ≥0对x∈(0,+∞)恒成立,求a的取值范围
≥0对x∈(0,+∞)恒成立,求a的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年银川一中二模理)设方程![]() ,(θ为参数).表示的曲线为C,
,(θ为参数).表示的曲线为C,
(1)求曲线C上的动点到原点O的距离的最小值
(2)点P为曲线C上的动点,当|OP|最小时(O为坐标原点),求点P的坐标。
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年银川一中二模文) (12分)已知函数![]() .
.
(1)若a,b都是从0,1,2,3,4五个数中任取的一个数,求上述函数有零点的概率.
(2)若a,b都是从区间[0,4]任取的一个数,求f(1)>0成立时的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com