
(本题14分)已知圆 和点
和点
(1)若过点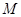 有且只有一条直线与圆
有且只有一条直线与圆 相切,求实数
相切,求实数 的值,并求出切线方程;
的值,并求出切线方程;
(2)若 ,过点
,过点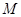 作圆的两条弦
作圆的两条弦 ,且
,且 互相垂直,求
互相垂直,求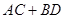 的最大值。
的最大值。
(1) 或即
或即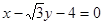 。(2)
。(2)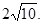
【解析】本试题主要是考查了直线与圆的位置关系的运用。
(1)因为圆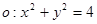 和点
和点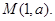 ,若过点
,若过点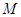 有且只有一条直线与圆
有且只有一条直线与圆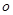 相切,则联立方程组只有一个实数解得到切线方程。
相切,则联立方程组只有一个实数解得到切线方程。
(2)若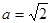 ,过点
,过点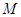 作圆的两条弦
作圆的两条弦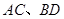 ,且
,且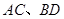 互相垂直,设
互相垂直,设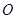 到直线
到直线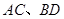 的距离分别为
的距离分别为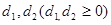 ,则
,则 于是
于是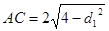 ,
,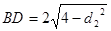 ,所以
,所以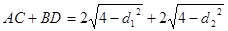 则
则 ,则利用不等式得到结论。
,则利用不等式得到结论。
解:(1)由条件知点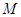 在圆
在圆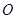 上,所以
上,所以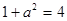 ,则
,则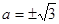 。当
。当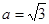 时,点
时,点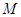 为
为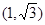 ,
,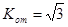 ,
,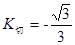 此时切线方程为
此时切线方程为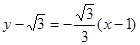 ,即
,即 。当
。当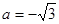 时,点
时,点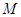 为
为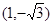 ,
,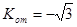 ,
, 此时切线方程为
此时切线方程为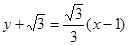 ,即
,即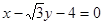 。所以所求的切线方程为
。所以所求的切线方程为 或即
或即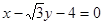 。-------------6分
。-------------6分
(2)设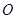 到直线
到直线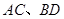 的距离分别为
的距离分别为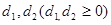 ,则
,则 于是
于是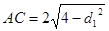 ,
,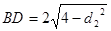 ,所以
,所以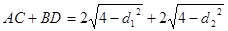 则
则 ,因为
,因为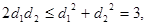 ,所以
,所以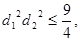 ,当且仅当
,当且仅当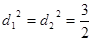 时取等号,所以
时取等号,所以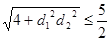 ,所以
,所以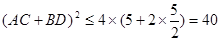 ,所以
,所以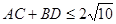 ,即
,即
的最大值为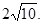 --------------------14分
--------------------14分


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源: 题型:
(本题14分)已知直线![]() :y=kx+1与双曲线C:2x2-y2=1的右支交于不同的两点A、B。(1)求实数k的取值范围;(2)是否存在实数k,使得以线段AB为直径的圆经过双曲线C的右焦点F?若荐在,求出k的值。若不存在,说明理由。
:y=kx+1与双曲线C:2x2-y2=1的右支交于不同的两点A、B。(1)求实数k的取值范围;(2)是否存在实数k,使得以线段AB为直径的圆经过双曲线C的右焦点F?若荐在,求出k的值。若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源:2014届广东省高一年级第二学期5月月考数学试卷(解析版) 题型:解答题
(本题满分14分)已知圆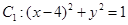 ,圆
,圆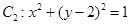 ,动点
,动点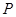 到圆
到圆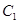 ,
,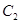 上点的距离的最小值相等.
上点的距离的最小值相等.
(1)求点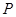 的轨迹方程;
的轨迹方程;
(2)点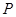 的轨迹上是否存在点
的轨迹上是否存在点 ,使得点
,使得点 到点
到点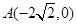 的距离减去点
的距离减去点 到点
到点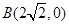 的距离的差为
的距离的差为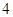 ,如果存在求出
,如果存在求出 点坐标,如果不存在说明理由.
点坐标,如果不存在说明理由.
查看答案和解析>>
科目:高中数学 来源:2013届江苏省淮安七校高二上学期期中考试理科数学 题型:解答题
(本题满分14分)
已知圆 内有一点
内有一点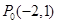 ,AB为过点
,AB为过点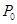 且倾斜角为α的弦,
且倾斜角为α的弦,
(1)当α=135º时,求直线AB的方程
(2)若弦AB被点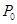 平分,求直线AB的方程。
平分,求直线AB的方程。
查看答案和解析>>
科目:高中数学 来源:2014届广东省湛江市高一第一学期第二学段考试数学 题型:解答题
(本题14分)已知与圆C: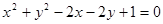 相切的直线
相切的直线 交x轴、y轴于A、B两点,O为原点,|OA|=3,|OB|=b(b>2).
交x轴、y轴于A、B两点,O为原点,|OA|=3,|OB|=b(b>2).
(1) 求b的值;
(2) 求△ABC的外接圆方程。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com