
【题目】已知函数f(x)为二次函数,且f(x-1)+f(x)=2x2+4.
(1)求f(x)的解析式;
(2)当x∈[t,t+2],t∈R时,求函数f(x)的最小值(用t表示).
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=1﹣nan(n∈N*)
(1)计算a1 , a2 , a3 , a4;
(2)猜想an的表达式,并用数学归纳法证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,其中a>0且a≠1.若a=
,其中a>0且a≠1.若a= ![]() 时方程f(x)=b有两个不同的实根,则实数b的取值范围是;若f(x)的值域为[2,+∞),则实数a的取值范围是 .
时方程f(x)=b有两个不同的实根,则实数b的取值范围是;若f(x)的值域为[2,+∞),则实数a的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=2017x+sin2017x,g(x)=log2017x+2017x , 则( )
A.对于任意正实数x恒有f(x)≥g(x)
B.存在实数x0 , 当x>x0时,恒有f(x)>g(x)
C.对于任意正实数x恒有f(x)≤g(x)
D.存在实数x0 , 当x>x0时,恒有f(x)<g(x)
查看答案和解析>>
科目:高中数学 来源: 题型:
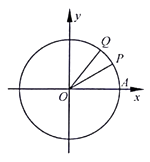
【题目】设A是单位圆O和x轴正半轴的交点,P,Q是圆O上两点,O为坐标原点,∠AOP= ![]() ,∠AOQ=α,α∈[0,
,∠AOQ=α,α∈[0, ![]() ].
]. 
(1)若Q( ![]() ,
, ![]() ),求cos(α﹣
),求cos(α﹣ ![]() )的值;
)的值;
(2)设函数f(α)=sinα( ![]()
![]() ),求f(α)的值域.
),求f(α)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】端午节小长假期间,张洋与几位同学从天津乘火车到大连去旅游,若当天从天津到大连的三列火车正点到达的概率分别为0.8,0.7,0.9,假设这三列火车之间是否正点到达互不影响,则这三列火车恰好有两列正点到达的概率是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥S﹣ABC中,SB⊥底面ABC,且SB=AB=2,BC= ![]() ,D、E分别是SA、SC的中点.
,D、E分别是SA、SC的中点. 
(Ⅰ)求证:平面ACD⊥平面BCD;
(Ⅱ)求二面角S﹣BD﹣E的平面角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣1|﹣|x+1|.
(1)求不等式|f(x)|<1的解集;
(2)若不等式|a|f(x)≥|f(a)|对任意a∈R恒成立,求实数x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com