
【题目】已知函数f(x)= ![]() ,其中a>0且a≠1.若a=
,其中a>0且a≠1.若a= ![]() 时方程f(x)=b有两个不同的实根,则实数b的取值范围是;若f(x)的值域为[2,+∞),则实数a的取值范围是 .
时方程f(x)=b有两个不同的实根,则实数b的取值范围是;若f(x)的值域为[2,+∞),则实数a的取值范围是 .
【答案】["(2, ![]() )","[
)","[ ![]() ,1)∪(1,+∞)"]
,1)∪(1,+∞)"]
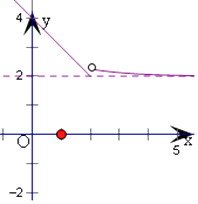
【解析】解:作出f(x)= ![]() 的图象,
的图象,
由a= ![]() 时方程f(x)=b有两个不同的实根,
时方程f(x)=b有两个不同的实根,
可得b>2,且b<2+0.52= ![]() ,
,
即有b∈(2, ![]() );
);
函数f(x)= ![]() ,
,
当0<a<1时,x≤2时,f(x)=4﹣x≥2,
x>2时,f(x)=ax+2a+1递减,
可得2a+1<f(x)<a2+2a+1,
f(x)的值域为[2,+∞),可得2a+1≥2,解得 ![]() ≤a<1;
≤a<1;
当a>1时,x≤2时,f(x)=4﹣x≥2,
x>2时,f(x)=ax+2a+1递增,
可得f(x)>a2+2a+1>4,
则f(x)的值域为[2,+∞)成立,a>1恒成立.
综上可得a∈[ ![]() ,1)∪(1,+∞).
,1)∪(1,+∞).
所以答案是:(2, ![]() ),[
),[ ![]() ,1)∪(1,+∞).
,1)∪(1,+∞).


科目:高中数学 来源: 题型:
【题目】设函数f(x)=log2x+ax+b(a>0),若存在实数b,使得对任意的x∈[t,t+2](t>0)都有|f(x)|≤1+a,则t的最小值是( )
A.2
B.1
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平行四边形ABCD中,A(1,2),B(2,1),中心E(3,3).
(1)判断平行四边形ABCD是否为正方形;
(2)点P(x,y)在平行四边形ABCD的边界及内部运动,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)为二次函数,且f(x-1)+f(x)=2x2+4.
(1)求f(x)的解析式;
(2)当x∈[t,t+2],t∈R时,求函数f(x)的最小值(用t表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要建造一个容积为1 600立方米,深为4米的长方体无盖蓄水池,池壁的造价为每平方米200元,池底的造价为每平方米100元.
(1)把总造价y元表示为池底的一边长x米的函数;
(2)由于场地原因,蓄水池的一边长不能超过20米,问蓄水池的这个底边长为多少时总造价最低?总造价最低是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com