
【题目】下列推理不属于合情推理的是( )
A. 由铜、铁、铝、金、银等金属能导电,得出一切金属都能导电.
B. 半径为![]() 的圆面积
的圆面积![]() ,则单位圆面积为
,则单位圆面积为![]() .
.
C. 由平面三角形的性质推测空间三棱锥的性质.
D. 猜想数列2,4,8,…的通项公式为![]() .
. ![]() .
.
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】把一个均匀的正方体骰子抛掷两次,观察出现的点数,记第一次出现的点数为![]() ,第二次出现的点数为
,第二次出现的点数为![]() ,设直线
,设直线![]() :
:![]() ,直线
,直线![]() :
:![]() .
.
(1)求直线![]() 和直线
和直线![]() 没有交点的概率;
没有交点的概率;
(2)求直线![]() 和直线
和直线![]() 的交点在第一象限的概率.
的交点在第一象限的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方体![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 分别在
分别在![]() 上,
上,![]()
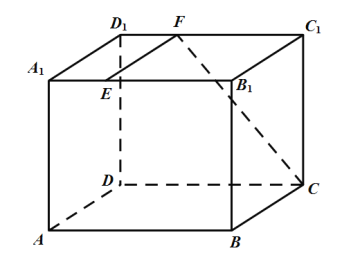
(1)求直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(2)过点![]() 的平面
的平面![]() 与此长方体的表面相交,交线围成一个正方形,求平面
与此长方体的表面相交,交线围成一个正方形,求平面![]() 把该长方体分成的两部分体积的比值.
把该长方体分成的两部分体积的比值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的两个焦点分别为F1,F2,短轴的一个端点为P,△PF1F2内切圆的半径为
=1(a>b>0)的两个焦点分别为F1,F2,短轴的一个端点为P,△PF1F2内切圆的半径为![]() ,设过点F2的直线l与被椭圆C截得的线段为RS,当l⊥x轴时,|RS|=3.
,设过点F2的直线l与被椭圆C截得的线段为RS,当l⊥x轴时,|RS|=3.
(1) 求椭圆C的标准方程;
(2) 若点M(0,m),(![]() ),过点M的任一直线与椭圆C相交于两点A.B,y轴上是否存在点N(0,n)使∠ANM=∠BNM恒成立?若存在,判断m、n应满足关系;若不存在,说明理由。
),过点M的任一直线与椭圆C相交于两点A.B,y轴上是否存在点N(0,n)使∠ANM=∠BNM恒成立?若存在,判断m、n应满足关系;若不存在,说明理由。
(3) 在(2)条件下m=1时,求△ABN面积的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某食品公司研发生产一种新的零售食品,从产品中抽取200件作为样本,测量这些产品的一项质量指标值,由测量结果得到如下的频率分布直方图:
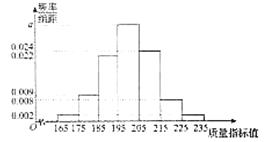
(1)求直方图中![]() 的值;
的值;
(2)由频率分布直方图可认为,这种产品的质量指标值![]() 服从正态分布
服从正态分布![]() ,试计算这批产品中质量指标值落在
,试计算这批产品中质量指标值落在![]() 上的件数;
上的件数;
(3)设产品的生产成本为![]() ,质量指标值为
,质量指标值为![]() ,生产成本与质量指标值满足函数关系式
,生产成本与质量指标值满足函数关系式![]() ,假设同组中的每个数据用该组数据区间的右端点代替,试计算生产该食品的平均成本.参考数据:若
,假设同组中的每个数据用该组数据区间的右端点代替,试计算生产该食品的平均成本.参考数据:若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的个数是_________.
(1)命题“若![]() ,则方程
,则方程![]() 有实数根”的逆否命题为“若方程
有实数根”的逆否命题为“若方程![]() 无实数根,则
无实数根,则![]() ”.
”.
(2)命题“![]() ,
,![]() ”的否定“
”的否定“![]() ,
,![]() ”.
”.
(3)若![]() 为假命题,则
为假命题,则![]() ,
,![]() 均为假命题.
均为假命题.
(4)“![]() ”是“直线
”是“直线![]() :
:![]() 与直线
与直线![]() :
:![]() 平行”的充要条件.
平行”的充要条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 分别是椭圆
分别是椭圆![]() 的左右焦点.
的左右焦点.
(Ⅰ)若![]() 是第一象限内该椭圆上的一点,
是第一象限内该椭圆上的一点,![]() ,求点
,求点![]() 的坐标.
的坐标.
(Ⅱ)若直线![]() 与圆
与圆![]() 相切,交椭圆
相切,交椭圆![]() 于
于![]() 两点,是否存在这样的直线
两点,是否存在这样的直线![]() ,使得
,使得![]() ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com