
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的最小值;
的最小值;
(2)若函数![]() 的最小值为
的最小值为![]() ,令
,令![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)当![]() 时,易求得
时,易求得![]() 的解析式,为分段函数,由解析式易得当
的解析式,为分段函数,由解析式易得当![]() 时,
时,![]() ;(2)根据题意可求得
;(2)根据题意可求得![]() 的解析式,也是一分段函数,从而可求得其最小值为
的解析式,也是一分段函数,从而可求得其最小值为![]() ,根据题意,即可求得
,根据题意,即可求得![]() 的取值范围.
的取值范围.
试题解析: (1)![]() .................2分
.................2分
由![]() .................3分
.................3分
由![]() .................4分
.................4分
所以![]() ;.................5分
;.................5分
(2) ![]() .................6分
.................6分
当![]() .................7分
.................7分
当![]() .................8分
.................8分
当![]() .................9分
.................9分
所以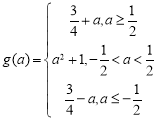 ..................10分
..................10分
又![]() ,所以当
,所以当![]() 时
时![]() ;当
;当![]() 时
时![]() ;当
;当![]() 时
时![]() ;
;
从而得![]() .................12分
.................12分


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
【题目】求适合下列条件的直线方程:
(1)经过点P(3,2)且在两坐标轴上的截距相等;
(2)经过点A(-1,-3),倾斜角等于直线y=3x的倾斜角的2倍.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是等腰三角形,
是等腰三角形,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 上一点.
上一点.
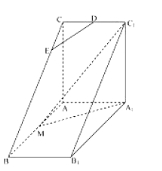
(I)若![]() 平面
平面![]() ,求
,求![]() ;
;
(II)平面![]() 将三棱柱
将三棱柱![]() 分成两个部分,求较小部分与较大部分的体积之比.
分成两个部分,求较小部分与较大部分的体积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某服装厂每天的固定成本是30000元,每天最大规模的生产量是![]() 件.每生产一件服装,成本增加100元,生产
件.每生产一件服装,成本增加100元,生产![]() 件服装的收入函数是
件服装的收入函数是![]() ,记
,记![]() ,
,![]() 分别为每天生产
分别为每天生产![]() 件服装的利润和平均利润(
件服装的利润和平均利润(![]() ).
).
(1)当![]() 时,每天生产量
时,每天生产量![]() 为多少时,利润
为多少时,利润![]() 有最大值;
有最大值;
(2)每天生产量![]() 为多少时,平均利润
为多少时,平均利润![]() 有最大值,并求
有最大值,并求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com