
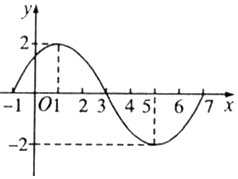
 已知函数y=Asin(ωx+φ)(A>0,ω>0)在一个周期内的图象如图所示.
已知函数y=Asin(ωx+φ)(A>0,ω>0)在一个周期内的图象如图所示.分析 (1)由图知A,T,利用周期公式可求ω,又图象过点(1,2),利用五点作图法可求φ,即可得解函数解析式.
(2)根据函数y=Asin(ωx+∅)的图象变换规律,得出结论.
解答 解:(1)由图知A=2,T=8,
∴ω=$\frac{π}{4}$.
∴y=2sin($\frac{π}{4}$x+φ).
又∵图象过点(1,2),
∴sin( $\frac{π}{4}$+φ)=1.
∴φ=$\frac{π}{4}$.
∴y=2sin($\frac{π}{4}$x+$\frac{π}{4}$).
(2)将y=sinx图象上所有点的横坐标保持不变,将纵坐标增大为原来的2倍,得到y=2sinx.
又将y=2sinx向左平移$\frac{π}{4}$个单位,得到y=2sin(x+$\frac{π}{4}$).
再将y=2sin(x+$\frac{π}{4}$)纵坐标不变,横坐标变为原来的$\frac{4}{π}$倍,得到y=2sin($\frac{π}{4}$x+$\frac{π}{4}$).
点评 本题主要考查利用y=Asin(ωx+∅)的图象特征,由函数y=Asin(ωx+∅)的部分图象求解析式,y=Asin(ωx+∅)的图象变换规律,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | 0 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 66 | 69 | 73 | 81 | 89 | 90 | 91 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 商店名称 | A | B | C | D | E |
| 销售额x(千万元) | 3 | 5 | 6 | 7 | 9 |
| 利润额y(百万元) | 2 | 3 | 3 | 4 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 32 | C. | 16 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com