练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．两圆x2+y2-6x+16y-48=0与x2+y2+4x-8y-44=0的公切线条数为（　　）
    A．4条B．3条C．2条D．1条

    分析 将两圆化成标准方程，可得它们的圆心坐标和半径大小，从而得到两圆的圆心距等于13，恰好介于两圆的半径差与半径和之间，由此可得两圆位置关系是相交，从而得到它们有两条公切线．

    解答 解：∵圆C1：x2+y2-6x+16y-48=0化成标准方程，得（x-3）2+（y+8）2=121
    ∴圆C1的圆心坐标为（3，-8），半径r1=11
    同理，可得圆C2的圆心坐标为（-2，4），半径r2=8
    因此，两圆的圆心距|C1C2|=$\sqrt{（3+2）^{2}+（-8-4）^{2}}$=13
    ∵|r1-r2|＜|C1C2|＜r1+r2=16
    ∴两圆的位置关系是相交，可得两圆有2条公切线
    故选：C

    点评 本题给出两个圆的一般式方程，探求两圆的位置关系并找出公切线的条数，着重考查了圆的一般式方程与标准方程的互化和两圆位置关系的判断等知识点，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    2．已知f（x）=3x-2，若f（x）的图象关于点A（2，1）对称的图象对应的函数为g（x），则g（x）的表达式为g（x）=3x-8．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．已知直线l的点斜式方程为y+2=$\sqrt{3}$（x+1），则此直线的倾斜角为（　　）
    A．30°B．60°C．120°D．150°

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．若集合P={-2，0，2}，i是虚数单位，则（　　）
    A．2i∈PB．$\frac{2}{i}$∈PC．（$\sqrt{2}$i）2∈PD．$\frac{2}{{i}^{3}}$∈P

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知等差数列{an}，公差d不为零，a1=1，且a2，a5，a14成等比数列．
    （Ⅰ）求数列{an}，的通项公式；
    （Ⅱ）设数列{bn}，满足bn=$\frac{1}{{a}_{n}•{a}_{n+1}}$，求证：b1+b2+b3+…+bn＜$\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．下列不等式中，正确的是（　　）
    A．tan$\frac{4π}{7}$＞tan$\frac{3π}{7}$B．tan$\frac{2π}{5}$＜tan$\frac{3π}{5}$
    C．tan（-$\frac{13π}{7}$）＞tan（-$\frac{15π}{8}$）D．tan（-$\frac{13π}{4}$）＜tan（-$\frac{12π}{5}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．数列1，1，2，3，x，8，13，21，…中的x值为5．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

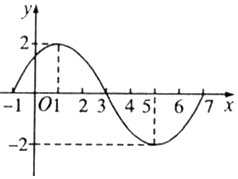    1．已知函数y=Asin（ωx+φ）（A＞0，ω＞0）在一个周期内的图象如图所示．
    （1）求它的解析式；
    （2）说明怎样由y=sinx图象平移得到．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知等比数列{an}的首项a1=$\frac{1}{3}$，公比q满足q＞0且q≠1，又已知a1，5a3，9a5成等差数列；
    （1）求数列{an}的通项公式；
    （2）令bn=log3$\frac{1}{a_n}$，记Tn=$\frac{1}{{{b_1}{b_2}}}+\frac{1}{{{b_2}{b_3}}}+\frac{1}{{{b_3}{b_4}}}+…+\frac{1}{{{b_n}{b_{n+1}}}}$，是否存在最大的整数m，使得对任意n∈N*，均有Tn＞$\frac{m}{16}$成立？若存在，求出m，若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案