
分析 (Ⅰ)找出满足条件的m,n的范围,利用区间长度比求概率;
(Ⅱ)求出满足条件的m,n的关系式,计算单元区域的面积,利用面积比求概率;
(Ⅲ)利用随机数模拟的方法,结合满足条件的随机次数,利用频率f=$\frac{{N}_{1}}{N}$,得出概率的近似值.
解答 解:(Ⅰ)m=1,方程x2+x+n2=0有实数根等价于△=1-4n2≥0即$-\frac{1}{2}$≤n≤$\frac{1}{2}$,…(1分)
由几何概型概率公式得方程有解的概率为P=$\frac{\frac{1}{2}-(-\frac{1}{2})}{1-(-1)}=\frac{1}{2}$.…(3分)
(Ⅱ)方程x2+mx+n2=0有实数根等价于△=m2-4n2≥0.即$\left\{\begin{array}{l}{m+2n≥0}\\{m-2n≥0}\end{array}\right.$或$\left\{\begin{array}{l}{m+2n≤0}\\{m-2n≤0}\end{array}\right.$.
设事件A={方程有实根},则A构成的区域面积为$2×\frac{1}{2}×1×1$=1
…(4分)
(m,n)可看成是平面内的点,试验的所有结果所构成的区域为Ω={(m,n)|-1≤m≤1,-1≤n≤1},
这是一个边长为2的正方形区域,面积为4,…(6分)
所以由几何概性概率告诉的关于x的方程x2+mx+n2=0有实数根的概率p=$\frac{{S}_{A}}{{S}_{Ω}}=\frac{1}{4}$.…(9分)
(Ⅲ)第一步:利用计算器或者计算机产生两组0到1之间的随机数:m=RAND,n=RAND;
第二步:统计试验的总次数N和满足条件“m2-4n2≥0”的次数N1;
第三步:计算频率f=$\frac{{N}_{1}}{N}$,得出概率的近似值为f=$\frac{{N}_{1}}{N}$.…(12分)
点评 本题考查了几何概型的概率求法;关键是正确选择几何测度,利用公式求概率.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
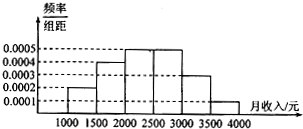 一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如图所示).为了进一步分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样的方法抽出100人作进一步调查,则在[2000,2500]月收入段应抽出( )
一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如图所示).为了进一步分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样的方法抽出100人作进一步调查,则在[2000,2500]月收入段应抽出( )| A. | 10人 | B. | 15人 | C. | 20人 | D. | 25人 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{3}{4}$,1) | B. | [$\frac{5}{7}$,1) | C. | [$\frac{9}{10}$,1) | D. | [$\frac{5}{7}$,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com