
【题目】如图,在三棱柱![]() 中,已知
中,已知![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() .
.
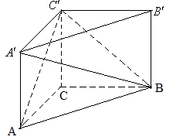
(1) 求证:![]() ;
;
(2) 求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)直棱柱的关系先证明![]() 和
和![]() 进而证明
进而证明![]() 平面
平面![]() ,从而得到
,从而得到![]() 即可.
即可.
(2)建立以![]() 为坐标原点,以
为坐标原点,以![]() ,
,![]() ,
,![]() 所在的直线分别为
所在的直线分别为![]() ,
,![]() ,
,![]() 轴的空间直角坐标系,再求出
轴的空间直角坐标系,再求出![]() 的向量与平面
的向量与平面![]() 的法向量求解即可.
的法向量求解即可.
解:(1)如图,连接![]() ,因为
,因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,![]() .
.
又![]() ,所以四边形
,所以四边形![]() 为正方形,所以
为正方形,所以![]() .
.
因为![]() ,所以
,所以![]() .又
.又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,所以,
,所以,![]() 平面
平面![]()
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]()
(2)解法1:在![]() 中,
中,![]() ,
,![]() ,
,![]() ,所以
,所以![]() .
.
又![]() 平面
平面![]() ,
,![]() ,所以三棱锥
,所以三棱锥![]() 的体积
的体积![]()
易知![]() ,
,![]() ,
,![]() ,
,
所以![]()
设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,则三棱锥
,则三棱锥![]() 的体积
的体积![]() ,
,
由等体积法可知![]() ,则
,则![]() ,解得
,解得![]() .
.
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,则
,则![]() ,
,
故直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]()
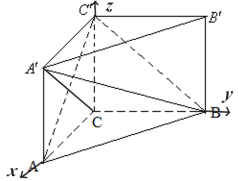
解法2:(2)由(1)知,![]() ,
,![]() ,
,![]() 两两垂直,以
两两垂直,以![]() 为坐标原点,以
为坐标原点,以![]() ,
,![]() ,
,![]() 所在的直线分别为
所在的直线分别为![]() ,
,![]() ,
,![]() 轴,建立如图所示的空间直角坐标系.因为
轴,建立如图所示的空间直角坐标系.因为![]() ,
,![]() .
.
所以![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]()
设平面![]() 的法向量为
的法向量为![]() ,则
,则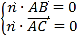 ,即
,即![]() ,
,
令![]() ,
,![]() ,所以
,所以![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
则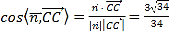
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,则
,则![]() ,
,
故直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]()
(1)若函数f(x)有两个零点,求实数a的取值范围;
(2)若a=3,且对任意的x1∈[-1,2],总存在![]() ,使g(x1)-f(x2)=0成立,求实数m的取值范围.
,使g(x1)-f(x2)=0成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,长轴长为
,长轴长为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程及离心率;
的标准方程及离心率;
(Ⅱ)过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,若点
两点,若点![]() 满足
满足![]() ,求证:由点
,求证:由点![]() 构成的曲线
构成的曲线![]() 关于直线
关于直线![]() 对称.
对称.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某公司生产某款手机的年固定成本为40万元,每生产1万只还需另投入16万元.设该公司一年内共生产该款手机![]() 万只并全部销售完,每万只的销售收入为
万只并全部销售完,每万只的销售收入为![]() 万元,且
万元,且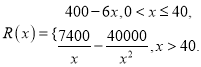
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (万只)的函数解析式;
(万只)的函数解析式;
(2)当年产量为多少万只时,该公司在该款手机的生产中所获得的利润最大?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】省环保厅对![]() 、
、![]() 、
、![]() 三个城市同时进行了多天的空气质量监测,测得三个城市空气质量为优或良的数据共有180个,三城市各自空气质量为优或良的数据个数如下表所示:
三个城市同时进行了多天的空气质量监测,测得三个城市空气质量为优或良的数据共有180个,三城市各自空气质量为优或良的数据个数如下表所示:
|
|
| |
优(个) | 28 |
|
|
良(个) | 32 | 30 |
|
已知在这180个数据中随机抽取一个,恰好抽到记录![]() 城市空气质量为优的数据的概率为0.2.
城市空气质量为优的数据的概率为0.2.
(1)现按城市用分层抽样的方法,从上述180个数据中抽取30个进行后续分析,求在![]() 城中应抽取的数据的个数;
城中应抽取的数据的个数;
(2)已知![]() ,
, ![]() ,求在
,求在![]() 城中空气质量为优的天数大于空气质量为良的天数的概率.
城中空气质量为优的天数大于空气质量为良的天数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个函数![]() ,如果对任意一个三角形,只要它的三边长
,如果对任意一个三角形,只要它的三边长![]() 、
、![]() 、
、![]() 都在
都在![]() 的定义域内,就有
的定义域内,就有![]() 、
、![]() 、
、![]() 也是某个三角形的三边长,则称
也是某个三角形的三边长,则称![]() 为“双三角形函数”.
为“双三角形函数”.
(1)判断![]() ,
,![]() ,
,![]() 中,哪些是“双三角形函数”,哪些不是,并说明理由;
中,哪些是“双三角形函数”,哪些不是,并说明理由;
(2)若![]() 是定义在
是定义在![]() 上周期函数,值域为
上周期函数,值域为![]() ,求证:
,求证:![]() 不是“双三角形函数”;
不是“双三角形函数”;
(3)已知函数![]() ,
,![]() ,求证:函数
,求证:函数![]() 是“双三角形函数”.(可利用公式“
是“双三角形函数”.(可利用公式“![]() ”)
”)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com