【题目】
为等差数列，则使等式
能成立的数列的项数
的最大值为_________；
【答案】50
【解析】
根据题意得到数列项数为偶数设为
，根据关系得到
，计算得到关系式
，计算得到答案.
{an}为等差数列，则使等式|a1|+|a2|+…+|an|，
＝|a1+1|+|a2+1|+…+|an+1|，
＝|a1+2|+|a2+2|+…+|an+2|，
＝|a1+3|+|a2+3|+…+|an+3|，
则：数列{an}中的项一定满足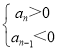
或
，
且项数n为偶数，
设n＝2k，等差数列的公差为d，首项为a1，
不妨设
，
则：a1＜0，d＞0，
且：ak+3＜0，
由
，
可得d＞3，
所以：|a1|+|a2|+..+|an|＝﹣a1﹣a2﹣a3﹣…﹣ak+ak+1+ak+2+…+a2k，
＝﹣2（a1+a2+a3+…+ak）+（a1+a2+a3+…+ak+ak+1+…+a2k）
＝﹣2（
）+（
），
＝k2d＝2018，
由于：d＞3，
所以：k2d＝2018＞3d2，
解得：k2＜672，
故：k≤25，
故：n≤50．
故答案为：50．
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目：高中数学 来源： 题型：
【题目】已知
（
（1）当a＝0时，求f（x）的极值；
（2）当a＞0时，讨论f（x）的单调性；
（3）若对任意的a∈（2, 3），x1, x2∈[1, 3]，恒有（m－ln3）a－2ln3＞|f（x1）－f（x2）|成立，求实数m的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知常数
，数列
满足
，
.
(1)若
，
，求
的值；
(2)在(1)的条件下，求数列的前
项和
；
(3)若数列中存在三项
，
，
(
且
)依次成等差数列,求
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
是奇函数（其中
）
（1）求实数m的值；
（2）已知关于x的方程
在区间
上有实数解，求实数k的取值范围；
（3）当
时，
的值域是
，求实数n与a的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知
为定义在实数集
上的函数，把方程
称为函数
的特征方程，特征方程的两个实根
、
（
），称为的特征根.
（1）讨论函数的奇偶性，并说明理由；
（2）已知
为给定实数，求
的表达式；
（3）把函数
，
的最大值记作
，最小值记作
，研究函数，的单调性，令
，若
恒成立，求
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】记无穷数列
的前
项中最大值为
，最小值为
，令
，
.
（1）若
，请写出
的值；
（2）求证：“数列是等差数列”是“数列
是等差数列”的充要条件；
（3）若对任意，有
，且
，请问：是否存在
，使得对于任意不小于
的正整数，有
成立？请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】由9个正数组成的矩阵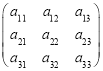
中，每行中三个数成等差数列，且
、
、
成等比数列，给出下列判断：① 第2列中，
、
、
必成等比数列；② 第1列中的
、
、
不一定成等比数列；③ 
；④ 若9个数之和等于9，则
；其中正确的个数为（ ）
A.1B.2C.3D.4
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】给定函数
和
，令
，对以下三个论断：
（1）若和都是奇函数，则
也是奇函数；（2）若和都是非奇非偶函数，则也是非奇非偶函数：（3）和之一与有相同的奇偶性；其中正确论断的个数为（ ）
A.0个B.1个C.2个D.3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
