
【题目】已知常数![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() 的值;
的值;
(2)在(1)的条件下,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)若数列![]() 中存在三项
中存在三项![]() ,
,![]() ,
,![]() (
(![]() 且
且![]() )依次成等差数列,求
)依次成等差数列,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据题中条件,逐项计算,即可得出结果;
(2)由(1)得到![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,从而
,从而![]() ,得出
,得出![]() ,由等比数列的求和公式,即可得出结果;
,由等比数列的求和公式,即可得出结果;
(3)先由![]() ,得到数列
,得到数列![]() 是递增数列,分
是递增数列,分![]() ,
,![]() ,
,![]() 三种情况,利用放缩法,以及等差中项的概念,即可得出结果.
三种情况,利用放缩法,以及等差中项的概念,即可得出结果.
(1)因为![]() ,
,![]() ,
,
所以![]() ,
,
因此![]() ,
,![]() ,
,
![]() ;
;
(2)因为![]() ,
,![]() ,
,
所以,当![]() 时,
时,![]() ,从而
,从而![]() ,
,
于是有:![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
所以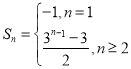 ,即
,即![]() ,
,![]() ;
;
(3)因为![]() ,
,
所以![]() ,即数列
,即数列![]() 是递增数列,
是递增数列,
①当![]() 时,有
时,有![]() ,于是有
,于是有![]() ,
,
从而![]() ,
,
所以![]() ,
,
若数列![]() 中存在三项
中存在三项![]() ,
,![]() ,
,![]() (
(![]() 且
且![]() )依次成等差数列,
)依次成等差数列,
则有![]() ,即
,即![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() 不成立,因此此时数列
不成立,因此此时数列![]() 中不存在三项
中不存在三项![]() ,
,![]() ,
,![]() (
(![]() 且
且![]() )依次成等差数列;
)依次成等差数列;
②当![]() 时,有
时,有![]() ,
,
此时![]() ,
,
于是当![]() 时,
时,![]() ,从而
,从而![]() ,
,
所以![]() ,
,
若数列![]() 中存在三项
中存在三项![]() ,
,![]() ,
,![]() (
(![]() 且
且![]() )依次成等差数列,
)依次成等差数列,
则有![]() ,同①可知:
,同①可知:![]() ,于是有
,于是有![]() ,
,
因为![]() ,所以
,所以![]() ,
,
因为![]() 是整数,所以
是整数,所以![]() ,
,
于是![]() ,即
,即![]() 与
与![]() 矛盾,
矛盾,
故此时数列![]() 中不存在三项
中不存在三项![]() ,
,![]() ,
,![]() (
(![]() 且
且![]() )依次成等差数列;
)依次成等差数列;
③当![]() 时,有
时,有![]() ,
,![]() ,
,
于是![]() ,
,
![]() ,
,
此时数列![]() 中存在三项
中存在三项![]() ,
,![]() ,
,![]() (
(![]() 且
且![]() )依次成等差数列,
)依次成等差数列,
综上,![]() .
.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】平面直角坐标系中,直线![]() 的参数方程为
的参数方程为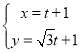 ,(
,(![]() 为参数).以原点为极点,
为参数).以原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的极坐标方程与曲线
的极坐标方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知与直线![]() 平行的直线
平行的直线![]() 过点
过点![]() ,且与曲线
,且与曲线![]() 交于
交于![]() 两点,试求
两点,试求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若有穷数列![]() (
(![]() )满足:①
)满足:①![]() ;②
;②![]() .则称该数列为“
.则称该数列为“![]() 阶非凡数列”
阶非凡数列”
(1)分别写出一个单调递增的“![]() 阶非凡数列”和一个单调递减的“
阶非凡数列”和一个单调递减的“![]() 阶非凡数列”;
阶非凡数列”;
(2)设![]() ,若“
,若“![]() 阶非凡数列”是等差数列,求其通项公式;
阶非凡数列”是等差数列,求其通项公式;
(3)记“![]() 阶非凡数列”的前
阶非凡数列”的前![]() 项的和为
项的和为![]() ,求证:
,求证:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位有员工1000名,平均每人每年创造利润10万元,为了增加企业竞争力,决定优化产业结构,调整出![]() (
(![]() )名员工从事第三产业,调整后这
)名员工从事第三产业,调整后这![]() 名员工他们平均每人创造利润为
名员工他们平均每人创造利润为![]() 万元,剩下的员工平均每人每年创造的利润可以提高
万元,剩下的员工平均每人每年创造的利润可以提高![]() .
.
(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整多少名员工从事第三产业?
(2)设![]() ,若调整出的员工创造出的年总利润始终不高于剩余员工创造的年总利润,求
,若调整出的员工创造出的年总利润始终不高于剩余员工创造的年总利润,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某海域有![]() 两个岛屿,
两个岛屿,![]() 岛在
岛在![]() 岛正东4海里处,经多年观察研究发现,某种鱼群洄游的路线是曲线
岛正东4海里处,经多年观察研究发现,某种鱼群洄游的路线是曲线![]() ,曾有渔船在距
,曾有渔船在距![]() 岛、
岛、![]() 岛距离和为8海里处发出过鱼群。以
岛距离和为8海里处发出过鱼群。以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 的垂直平分线为
的垂直平分线为![]() 轴建立平面直角坐标系.
轴建立平面直角坐标系.
(1)求曲线![]() 的标准方程;
的标准方程;
(2)某日,研究人员在![]() 两岛同时用声纳探测仪发出不同频率的探测信号(传播速度相同),
两岛同时用声纳探测仪发出不同频率的探测信号(传播速度相同),![]() 两岛收到鱼群在
两岛收到鱼群在![]() 处反射信号的时间比为
处反射信号的时间比为![]() ,问你能否确定
,问你能否确定![]() 处的位置(即点
处的位置(即点![]() 的坐标)?
的坐标)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于曲线![]() 所在的平面上的定点
所在的平面上的定点![]() ,若存在以点
,若存在以点![]() 为顶点的角
为顶点的角![]() ,使得
,使得![]() 对于曲线
对于曲线![]() 上的任意两个不同的点
上的任意两个不同的点![]() 恒成立,则称角
恒成立,则称角![]() 为曲线
为曲线![]() 的“
的“![]() 点视角”,并称其中最小的“
点视角”,并称其中最小的“![]() 点视角”为曲线
点视角”为曲线![]() 相对于点
相对于点![]() 的”
的”![]() 点确视角”.已知曲线
点确视角”.已知曲线![]() 和圆
和圆![]() 是
是![]() 轴上一点
轴上一点
(1)对于坐标原点![]() ,写出曲线
,写出曲线![]() 的“
的“![]() 点确视角”的大小;
点确视角”的大小;
(2)若![]() 在曲线
在曲线![]() 上,求
上,求![]() 的最小值;
的最小值;
(3)若曲线![]() 和圆
和圆![]() 的“
的“![]() 点确视角”相等,求
点确视角”相等,求![]() 点坐标.
点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】七巧板是古代中国劳动人民发明的一种中国传统智力玩具,它由五块等腰直角三角形,一块正方形和一块平行四边形共七块板组成.清陆以湉《冷庐杂识》卷一中写道:近又有七巧图,其式五,其数七,其变化之式多至千余.体物肖形,随手变幻,盖游戏之具,足以排闷破寂,故世俗皆喜为之.如图是一个用七巧板拼成的正方形,若在此正方形中任取一点,则此点取自阴影部分的概率为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com