【题目】由9个正数组成的矩阵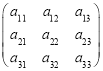
中，每行中三个数成等差数列，且
、
、
成等比数列，给出下列判断：① 第2列中，
、
、
必成等比数列；② 第1列中的
、
、
不一定成等比数列；③ 
；④ 若9个数之和等于9，则
；其中正确的个数为（ ）
A.1B.2C.3D.4
走进文言文系列答案科目：高中数学 来源： 题型：
【题目】省环保厅对
、
、
三个城市同时进行了多天的空气质量监测，测得三个城市空气质量为优或良的数据共有180个，三城市各自空气质量为优或良的数据个数如下表所示：
|
|
| |
优（个） | 28 |
|
|
良（个） | 32 | 30 |
|
已知在这180个数据中随机抽取一个，恰好抽到记录
城市空气质量为优的数据的概率为0.2.
（1）现按城市用分层抽样的方法，从上述180个数据中抽取30个进行后续分析，求在
城中应抽取的数据的个数；
（2）已知
， 
，求在
城中空气质量为优的天数大于空气质量为良的天数的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
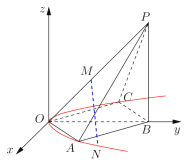
【题目】如图，空间直角坐标系中，四棱锥
的底面是边长为
的正方形，且底面在
平面内，点
在
轴正半轴上，
平面
，侧棱
与底面所成角为45°；
（1）若
是顶点在原点，且过
、
两点的抛物线上的动点，试给出
与满足的关系式；
（2）若
是棱上的一个定点，它到平面的距离为
（
），写出、
两点之间的距离
，并求的最小值；
（3）是否存在一个实数（），使得当取得最小值时，异面直线
与
互相垂直？请说明理由；
查看答案和解析>>
科目：高中数学 来源： 题型：
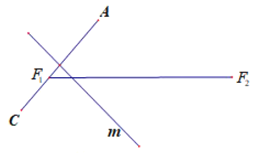
【题目】如图，已知平面内一动点
到两个定点
、
的距离之和为
，线段
的长为
.
（1）求动点的轨迹
的方程；
（2）过点作直线
与轨迹交于、
两点，且点在线段的上方，线段
的垂直平分线为
.
①求
的面积的最大值；
②轨迹上是否存在除、外的两点
、
关于直线对称，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】将所有平面向量组成的集合记作
，
是从到的映射，记作
或
，其中
都是实数.定义映射的模为:在
的条件下
的最大值记做
.若存在非零向量
，及实数
使得
，则称为的一个特征值.
（1）若
求；
（2）如果
,计算的特征值，并求相应的
；
（3）试找出一个映射，满足以下两个条件:①有唯一特征值，②
.(不需证明)
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一个函数
，如果对任意一个三角形，只要它的三边长
、
、
都在的定义域内，就有
、
、
也是某个三角形的三边长，则称为“双三角形函数”.
（1）判断
，
，
中，哪些是“双三角形函数”，哪些不是，并说明理由；
（2）若
是定义在
上周期函数，值域为
，求证：不是“双三角形函数”；
（3）已知函数
，
，求证：函数
是“双三角形函数”.（可利用公式“
”）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
