
分析 利用“乘1法”与基本不等式的性质即可得出.
解答 解:∵正实数x,y满足2x+y=2,
则$\frac{2}{x}$+$\frac{1}{y}$=$\frac{1}{2}(2x+y)$$(\frac{2}{x}+\frac{1}{y})$=$\frac{1}{2}(5+\frac{2y}{x}+\frac{2x}{y})$≥$\frac{1}{2}(5+2×2×\sqrt{\frac{y}{x}×\frac{x}{y}})$=$\frac{9}{2}$,当且仅当x=y=$\frac{2}{3}$时取等号.
∴$\frac{2}{x}$+$\frac{1}{y}$的最小值为$\frac{9}{2}$.
故答案为:$\frac{9}{2}$.
点评 本题考查了“乘1法”与基本不等式的性质,考查了推理能力与计算能力,属于基础题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | 3或-3 | B. | 3或4 | C. | -3或-1 | D. | -1或4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
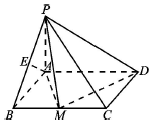 如图,四棱锥P-ABCD,底面ABCD为矩形,AB=PA=$\sqrt{3}$,AD=2,PB=$\sqrt{6}$,E为PB中点,且AE⊥PC.
如图,四棱锥P-ABCD,底面ABCD为矩形,AB=PA=$\sqrt{3}$,AD=2,PB=$\sqrt{6}$,E为PB中点,且AE⊥PC.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
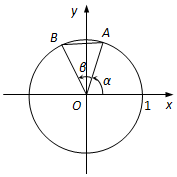 如图,在平面直角坐标系xOy中,以x轴正半轴为始边作锐角α,其终边与单位圆交于点A.以OA为始边作锐角β,其终边与单位圆交于点B,AB=$\frac{{2\sqrt{5}}}{5}$.
如图,在平面直角坐标系xOy中,以x轴正半轴为始边作锐角α,其终边与单位圆交于点A.以OA为始边作锐角β,其终边与单位圆交于点B,AB=$\frac{{2\sqrt{5}}}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
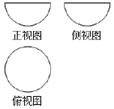 如图是某几何体的三视图,其正视图,侧视图均为直径为2的半圆,俯视图是直径为2的圆,则该几何体的表面积为( )
如图是某几何体的三视图,其正视图,侧视图均为直径为2的半圆,俯视图是直径为2的圆,则该几何体的表面积为( )| A. | 3π | B. | 4π | C. | 5π | D. | 12π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com