
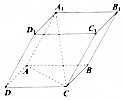
 如图,在平行六面体A1C中,AD=AB=AA1=4,∠A1AB=60°,∠BAD=90°,∠A1AD=120°,cos∠A1AC=( )
如图,在平行六面体A1C中,AD=AB=AA1=4,∠A1AB=60°,∠BAD=90°,∠A1AD=120°,cos∠A1AC=( )| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | 0 | D. | $\frac{1}{2}$ |
分析 运用向量的三角形法则和向量数量积的定义和性质:向量的平方即为模的平方,结合勾股定理的逆定理,计算即可得到所求余弦值.
解答 解:在平行六面体A1C中,AD=AB=AA1=4,∠A1AB=60°,
∠BAD=90°,∠A1AD=120°,
可得|$\overrightarrow{{A}_{1}C}$|2=|$\overrightarrow{{A}_{1}A}$+$\overrightarrow{AC}$|2=|$\overrightarrow{{A}_{1}A}$+$\overrightarrow{AB}$+$\overrightarrow{AD}$|2=|$\overrightarrow{{A}_{1}A}$|2+|$\overrightarrow{AB}$|2+|$\overrightarrow{AD}$|2+2$\overrightarrow{{A}_{1}A}$•$\overrightarrow{AB}$+2$\overrightarrow{AB}$•$\overrightarrow{AD}$+2$\overrightarrow{{A}_{1}A}$•$\overrightarrow{AD}$
=16+16+16+2×4×4×cos60°+2×4×4×cos90°+2×4×4×cos120°
=48+16+0-16=48,
又|$\overrightarrow{AC}$|2=|$\overrightarrow{AB}$|2+|$\overrightarrow{AD}$|2+2$\overrightarrow{AB}$•$\overrightarrow{AD}$=16+16+0=32,
|$\overrightarrow{{A}_{1}A}$|2+|$\overrightarrow{AC}$|2=16+32=48=|$\overrightarrow{{A}_{1}C}$|2,
即为$\overrightarrow{{A}_{1}A}$⊥$\overrightarrow{AC}$,
可得cos∠A1AC=0.
故选:C.
点评 本题考查角的余弦值的求法,注意运用向量法,以及向量数量积的定义和性质:向量的平方即为模的平方,考查勾股定理的逆定理,以及运算能力,属于中档题.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:选择题
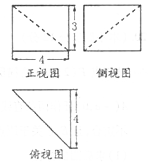
| A. | $\frac{\sqrt{34}}{2}$ | B. | $\frac{\sqrt{41}}{2}$ | C. | 17 | D. | 41 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
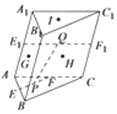 如图,在三棱柱ABC-A1B1C1中,E,F,E1,F1分别为棱AB,AC,AA1,CC1的中点,点G,H分别为四边形ABB1A1,BCC1B1对角线的交点,点I为△A1B1C1的外心,P,Q分别在直线EF,E1F1上运动,则在G,H,I,这三个点中,动直线PQ( )
如图,在三棱柱ABC-A1B1C1中,E,F,E1,F1分别为棱AB,AC,AA1,CC1的中点,点G,H分别为四边形ABB1A1,BCC1B1对角线的交点,点I为△A1B1C1的外心,P,Q分别在直线EF,E1F1上运动,则在G,H,I,这三个点中,动直线PQ( )| A. | 只可能经过点I | B. | 只可能经过点G,H | ||
| C. | 可能经过点G,H,I | D. | 不可能经过点G,H,I |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某公司2017年元旦晚会现场,为了活跃气氛,将在晚会节目表演过程中进行抽奖活动.
某公司2017年元旦晚会现场,为了活跃气氛,将在晚会节目表演过程中进行抽奖活动.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
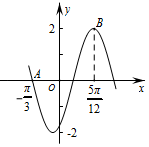 函数f(x)=Asin(ωx+ϕ),($A>0,ω>0,-\frac{π}{2}<ϕ<\frac{π}{2}$)的部分 图象如图所示,则函数f(x)的解析式为f(x)=2sin(2x$-\frac{π}{3}$).
函数f(x)=Asin(ωx+ϕ),($A>0,ω>0,-\frac{π}{2}<ϕ<\frac{π}{2}$)的部分 图象如图所示,则函数f(x)的解析式为f(x)=2sin(2x$-\frac{π}{3}$).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}+i}{2}$ | B. | -$\sqrt{3}$-i | C. | -$\sqrt{3}$+i | D. | -$\frac{\sqrt{3}+i}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com