
分析 (1)通过平面向量数量积的运算及三角函数的和角公式计算即可;
(2)通过$\overrightarrow{a}$•$\overrightarrow{b}$=cos2x、|$\overrightarrow{a}$+$\overrightarrow{b}$|=2cosx,利用换元法令t=cosx∈[0,1]可得f(x)=g(t)=2(t-λ)2-1-2λ2.分0≤λ≤1时、λ>1两种情况讨论即可.
解答 解:(1)∵向量$\overrightarrow{a}$=(cos$\frac{3x}{2}$,sin$\frac{3x}{2}$),$\overrightarrow{b}$=(cos$\frac{x}{2}$,-sin$\frac{x}{2}$),
∴$\overrightarrow{a}$•$\overrightarrow{b}$=(cos$\frac{3x}{2}$,sin$\frac{3x}{2}$)•(cos$\frac{x}{2}$,-sin$\frac{x}{2}$)
=cos$\frac{3x}{2}$cos$\frac{x}{2}$-sin$\frac{3x}{2}$sin$\frac{x}{2}$
=cos2x,
∵$\overrightarrow{a}$+$\overrightarrow{b}$=(cos$\frac{3x}{2}$,sin$\frac{3x}{2}$)+(cos$\frac{x}{2}$,-sin$\frac{x}{2}$)
=(cos$\frac{3x}{2}$+cos$\frac{x}{2}$,sin$\frac{3x}{2}$-sin$\frac{x}{2}$),
∴|$\overrightarrow{a}$+$\overrightarrow{b}$|2=cos2$\frac{3x}{2}$+cos2$\frac{x}{2}$+2cos$\frac{3x}{2}$cos$\frac{x}{2}$+sin2$\frac{3x}{2}$+sin2$\frac{x}{2}$-2sin$\frac{3x}{2}$sin$\frac{x}{2}$
=2+2cos$\frac{3x}{2}$cos$\frac{x}{2}$-2sin$\frac{3x}{2}$sin$\frac{x}{2}$
=2+2cos2x,
∴|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{2(1+cos2x)}$,
又∵x∈[0,$\frac{π}{2}$],∴cosx>0,
∴$\sqrt{2(1+cos2x)}$=$\sqrt{2(1+2co{s}^{2}x-1)}$=2cosx,
即|$\overrightarrow{a}$+$\overrightarrow{b}$|=2cosx;
(2)∵$\overrightarrow{a}$•$\overrightarrow{b}$=cos2x,|$\overrightarrow{a}$+$\overrightarrow{b}$|=2cosx,
∴f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$-2λ|$\overrightarrow{a}$+$\overrightarrow{b}$|
=cos2x-4λcosx
=2cos2x-4 λcosx-1
=2(cosx-λ)2-1-2λ2,
令t=cosx∈[0,1],则f(x)=g(t)=2(t-λ)2-1-2λ2.
①当0≤λ≤1时,当且仅当t=λ时,f(x)取得最小值,
g(λ)=-1-2λ2即-1-2λ2=-2,
∴λ=$\frac{\sqrt{2}}{2}$;
②当λ>1时,当且仅当t=1时f(x)取得最小值,g(1)=1-4λ,
即1-4λ=-2,∴λ=$\frac{3}{4}$<1,不合题意,舍去;
综上所述,λ=$\frac{\sqrt{2}}{2}$.
点评 本题是一道平面向量与三角函数的综合题,考查平面向量数量积的运算,考查运算求解能力,考查分类讨论的思想,注意解题方法的积累,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
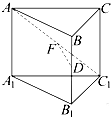 在棱长均相等的正三棱柱ABC-A1B1C1中,D为BB1的中点,F在AC1上,且DF⊥AC1,则下述结论:①AC1⊥BC;②AF=FC1;③平面DAC1⊥平面ACC1A1,其中正确的个数为( )
在棱长均相等的正三棱柱ABC-A1B1C1中,D为BB1的中点,F在AC1上,且DF⊥AC1,则下述结论:①AC1⊥BC;②AF=FC1;③平面DAC1⊥平面ACC1A1,其中正确的个数为( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com